Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 38 và 39 sách giáo khoa Toán 9 tập 2, chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi sắp tới.
Có một túi kín đựng 10 quả bóng, mỗi quả bóng có một trong các màu xanh, đỏ hoặc vàng. Thực hiện 30 lần lấy bóng, mỗi lần lấy 1 quả, ghi lại màu quả bóng được lấy ra sau đó trả lại bóng vào túi và trộn đều. a) Từ dữ liệu ghi lại, cho biết tần số xuất hiện của các quả bóng màu xanh, đỏ, vàng. Lập tỉ số giữa tần số và số lần lấy bóng. b) Đoán xem trong túi số lượng bóng màu gì là ít nhất, nhiều nhất.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 38SGK Toán 9 Kết nối tri thức
Có một túi kín đựng 10 quả bóng, mỗi quả bóng có một trong các màu xanh, đỏ hoặc vàng. Thực hiện 30 lần lấy bóng, mỗi lần lấy 1 quả, ghi lại màu quả bóng được lấy ra sau đó trả lại bóng vào túi và trộn đều.
a) Từ dữ liệu ghi lại, cho biết tần số xuất hiện của các quả bóng màu xanh, đỏ, vàng. Lập tỉ số giữa tần số và số lần lấy bóng.
b) Đoán xem trong túi số lượng bóng màu gì là ít nhất, nhiều nhất.
Phương pháp giải:
a) Thực hiện đủ 30 lần lấy bóng ra, ghi lại màu quả bóng rồi cho lại vào hộp. Thống kê số lần xuất hiện bóng màu xanh, bóng màu vàng và bóng màu đỏ. Từ đó ta thu được tần số xuất hiện của các quả bóng.
b) Màu quả bóng có tần số thấp nhất là ít nhất, màu quả bóng có tần số cao nhất là nhiều nhất.
Lời giải chi tiết:
a) Sau khi thực hiện 30 lần lấy bóng, ta thu được bảng tần số như sau:

Tỉ số giữa tần số quả bóng màu xanh và tần số lấy bóng là: \({f_X} = \frac{{15}}{{30}} = \frac{1}{2}\).
Tỉ số giữa tần số quả bóng màu đỏ và tần số lấy bóng là: \({f_Đ} = \frac{9}{{30}} = \frac{3}{{10}}\).
Tỉ số giữa tần số quả bóng màu vàng và tần số lấy bóng là: \({f_V} = \frac{6}{{30}} = \frac{1}{5}\).
b) Dự đoán rằng trong túi có số lượng bóng xanh là nhiều nhất, bóng vàng là ít nhất.
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 38 SGK Toán 9 Kết nối tri thức
Lập bảng tần số tương đối cho dãy dữ liệu thu được trong HĐ1.
Phương pháp giải:
Cho dãy dữ liệu \({x_1},{x_2},...,{x_n}\). Tần số tương đối \({f_i}\) của giá trị \({x_i}\) là tỉ số giữa tần số của \({x_i}\) (gọi là \({m_i}\)) với n.
Bảng sau đây được gọi là bảng tần số tương đối:

Trong đó \(n = {m_1} + ... + {m_k}\) và \({f_1} = \frac{{{m_1}}}{n}.100\left( \% \right)\) là tần số tương đối của \({x_1}\), …, \({f_k} = \frac{{{m_k}}}{n}.100\left( \% \right)\) là tần số tương đối của \({x_k}\).
Lời giải chi tiết:
Theo HĐ1, ta có: \({f_X} = \frac{1}{2} = 50\% ,{f_Đ} = \frac{3}{{10}} = 30\% ,{f_V} = \frac{1}{5} = 20\% \)
Ta có bảng tần số tương đối:

Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 39 SGK Toán 9 Kết nối tri thức
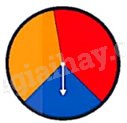
Quay 50 lần một tấm bìa hình tròn được chia thành ba hình quạt với các màu xanh, đỏ, vàng. Quan sát và ghi lại mũi tên chỉ vào hình quạt có màu nào khi tấm bìa dừng lại. Kết quả thu được như sau:

a) Lập bảng tần số tương đối cho kết quả thu được.
b) Ước lượng xác xuất mũi tên chỉ vào hình quạt màu đỏ.
Phương pháp giải:
a) + Tính tần số tương ứng với các giá trị trong mẫu dữ liệu.
+ Tính tần số tương đối ứng với các giá trị trong mẫu dữ liệu: Giá trị \({x_i}\) có tần số \({m_i}\) thì có tần số tương đối là: \({f_i} = \frac{{{m_i}}}{n}.100\left( \% \right)\) với m là tổng tất cả các tần số có trong mẫu số liệu.
+ Lập bảng tần số tương đối:
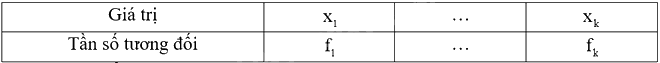
Lời giải chi tiết:
a) Tổng số quan sát là \(n = 50\). Số lần quay vào hình quạt màu xanh là: \({m_1} = 15\), số lần quay vào hình quạt màu đỏ là: \({m_2} = 25\), số lần quay vào hình quạt màu vàng là \({m_3} = 10\). Do đó, tần số tương đối cho các hình quạt màu xanh, màu đỏ, màu vàng lần lượt là: \({f_1} = \frac{{15}}{{50}} = 30\% ,{f_2} = \frac{{25}}{{50}} = 50\% ,{f_3} = \frac{{10}}{{50}} = 20\% \)
Ta có bảng tần số tương đối như sau:

b) Xác suất để mũi tên chỉ vào hình quạt màu đỏ là khoảng 50%.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 38SGK Toán 9 Kết nối tri thức
Có một túi kín đựng 10 quả bóng, mỗi quả bóng có một trong các màu xanh, đỏ hoặc vàng. Thực hiện 30 lần lấy bóng, mỗi lần lấy 1 quả, ghi lại màu quả bóng được lấy ra sau đó trả lại bóng vào túi và trộn đều.
a) Từ dữ liệu ghi lại, cho biết tần số xuất hiện của các quả bóng màu xanh, đỏ, vàng. Lập tỉ số giữa tần số và số lần lấy bóng.
b) Đoán xem trong túi số lượng bóng màu gì là ít nhất, nhiều nhất.
Phương pháp giải:
a) Thực hiện đủ 30 lần lấy bóng ra, ghi lại màu quả bóng rồi cho lại vào hộp. Thống kê số lần xuất hiện bóng màu xanh, bóng màu vàng và bóng màu đỏ. Từ đó ta thu được tần số xuất hiện của các quả bóng.
b) Màu quả bóng có tần số thấp nhất là ít nhất, màu quả bóng có tần số cao nhất là nhiều nhất.
Lời giải chi tiết:
a) Sau khi thực hiện 30 lần lấy bóng, ta thu được bảng tần số như sau:

Tỉ số giữa tần số quả bóng màu xanh và tần số lấy bóng là: \({f_X} = \frac{{15}}{{30}} = \frac{1}{2}\).
Tỉ số giữa tần số quả bóng màu đỏ và tần số lấy bóng là: \({f_Đ} = \frac{9}{{30}} = \frac{3}{{10}}\).
Tỉ số giữa tần số quả bóng màu vàng và tần số lấy bóng là: \({f_V} = \frac{6}{{30}} = \frac{1}{5}\).
b) Dự đoán rằng trong túi có số lượng bóng xanh là nhiều nhất, bóng vàng là ít nhất.
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 38 SGK Toán 9 Kết nối tri thức
Lập bảng tần số tương đối cho dãy dữ liệu thu được trong HĐ1.
Phương pháp giải:
Cho dãy dữ liệu \({x_1},{x_2},...,{x_n}\). Tần số tương đối \({f_i}\) của giá trị \({x_i}\) là tỉ số giữa tần số của \({x_i}\) (gọi là \({m_i}\)) với n.
Bảng sau đây được gọi là bảng tần số tương đối:

Trong đó \(n = {m_1} + ... + {m_k}\) và \({f_1} = \frac{{{m_1}}}{n}.100\left( \% \right)\) là tần số tương đối của \({x_1}\), …, \({f_k} = \frac{{{m_k}}}{n}.100\left( \% \right)\) là tần số tương đối của \({x_k}\).
Lời giải chi tiết:
Theo HĐ1, ta có: \({f_X} = \frac{1}{2} = 50\% ,{f_Đ} = \frac{3}{{10}} = 30\% ,{f_V} = \frac{1}{5} = 20\% \)
Ta có bảng tần số tương đối:

Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 39 SGK Toán 9 Kết nối tri thức
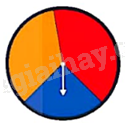
Quay 50 lần một tấm bìa hình tròn được chia thành ba hình quạt với các màu xanh, đỏ, vàng. Quan sát và ghi lại mũi tên chỉ vào hình quạt có màu nào khi tấm bìa dừng lại. Kết quả thu được như sau:

a) Lập bảng tần số tương đối cho kết quả thu được.
b) Ước lượng xác xuất mũi tên chỉ vào hình quạt màu đỏ.
Phương pháp giải:
a) + Tính tần số tương ứng với các giá trị trong mẫu dữ liệu.
+ Tính tần số tương đối ứng với các giá trị trong mẫu dữ liệu: Giá trị \({x_i}\) có tần số \({m_i}\) thì có tần số tương đối là: \({f_i} = \frac{{{m_i}}}{n}.100\left( \% \right)\) với m là tổng tất cả các tần số có trong mẫu số liệu.
+ Lập bảng tần số tương đối:
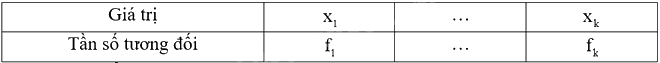
Lời giải chi tiết:
a) Tổng số quan sát là \(n = 50\). Số lần quay vào hình quạt màu xanh là: \({m_1} = 15\), số lần quay vào hình quạt màu đỏ là: \({m_2} = 25\), số lần quay vào hình quạt màu vàng là \({m_3} = 10\). Do đó, tần số tương đối cho các hình quạt màu xanh, màu đỏ, màu vàng lần lượt là: \({f_1} = \frac{{15}}{{50}} = 30\% ,{f_2} = \frac{{25}}{{50}} = 50\% ,{f_3} = \frac{{10}}{{50}} = 20\% \)
Ta có bảng tần số tương đối như sau:

b) Xác suất để mũi tên chỉ vào hình quạt màu đỏ là khoảng 50%.
Mục 1 trang 38, 39 SGK Toán 9 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc hai. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 yêu cầu học sinh xác định các hệ số a, b, c của hàm số bậc hai, tìm đỉnh của parabol, vẽ đồ thị hàm số và xác định khoảng đồng biến, nghịch biến của hàm số. Để giải bài tập này, học sinh cần nắm vững định nghĩa hàm số bậc hai, công thức tính đỉnh của parabol và các tính chất của hàm số.
Bài 2 tập trung vào việc giải các phương trình bậc hai bằng các phương pháp khác nhau, như sử dụng công thức nghiệm, phân tích thành nhân tử và sử dụng định lý Vi-et. Học sinh cần nắm vững các phương pháp giải phương trình bậc hai và lựa chọn phương pháp phù hợp cho từng bài toán cụ thể.
Bài 3 yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế, như tính quỹ đạo của vật được ném lên, tính diện tích của một hình chữ nhật có chu vi cho trước, và tìm giá trị lớn nhất hoặc nhỏ nhất của một biểu thức. Bài tập này giúp học sinh hiểu rõ hơn về ứng dụng của hàm số bậc hai trong đời sống.
Để giúp các em học sinh giải quyết các bài tập trong mục 1 trang 38, 39 SGK Toán 9 tập 2 - Kết nối tri thức một cách dễ dàng và hiệu quả, chúng tôi đã cung cấp lời giải chi tiết cho từng bài tập. Các lời giải này được trình bày một cách rõ ràng, dễ hiểu, kèm theo các bước giải cụ thể và các lưu ý quan trọng.
Ví dụ 1: Giải phương trình 2x2 - 5x + 2 = 0
Lời giải:
Ví dụ 2: Tìm đỉnh của parabol y = x2 - 4x + 3
Lời giải:
Đỉnh của parabol có tọa độ (x0, y0), trong đó x0 = -b / 2a = -(-4) / (2 * 1) = 2 và y0 = x02 - 4x0 + 3 = 22 - 4 * 2 + 3 = -1. Vậy, đỉnh của parabol là (2, -1).
Ngoài SGK Toán 9 tập 2 - Kết nối tri thức, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải toán:
Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 1 trang 38, 39 SGK Toán 9 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!