Giải bài tập 5.17 trang 98 SGK Toán 9 tập 1 - Kết nối tri thức

Bài tập 5.17 trang 98 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Giaitoan.edu.vn sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

Chúng tôi luôn cố gắng cung cấp nội dung chính xác, cập nhật và hữu ích nhất cho học sinh. Hãy cùng giaitoan.edu.vn khám phá lời giải bài tập 5.17 này nhé!

Cho đường tròn (O; 5 cm). a) Hãy nêu cách vẽ dây AB sao cho khoảng cách từ điểm O đến dây AB bằng 2,5 cm. b) Tính độ dài của dây AB trong câu a (làm tròn đến hàng phần trăm). c) Tính số đo và độ dài của cung nhỏ AB. d) Tính diện tích hình quạt tròn ứng với cung nhỏ AB.

Đề bài

Cho đường tròn (O; 5 cm).

a) Hãy nêu cách vẽ dây AB sao cho khoảng cách từ điểm O đến dây AB bằng 2,5 cm.

b) Tính độ dài của dây AB trong câu a (làm tròn đến hàng phần trăm).

c) Tính số đo và độ dài của cung nhỏ AB.

d) Tính diện tích hình quạt tròn ứng với cung nhỏ AB.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 5.17 trang 98 SGK Toán 9 tập 1 - Kết nối tri thức 1

a) Vẽ bán kính OM của đường tròn, trên OM lấy điểm H sao cho OH = 2,5 cm. Kẻ đoạn thẳng AB vuông góc với OH tại H.

b) Ta chứng minh \(AH = BH\) suy ra \(AB = 2AH\). Áp dụng định lý Pythagore để tính AH, từ đó suy ra độ dài AB.

c) Tính \(\sin \widehat {AOH}\) suy ra \(\widehat {AOH}\) và sđ\(\overset\frown{AB}\), từ đó tính được độ dài cung \(\overset\frown{AB}\).

d) Áp dụng công thức tính diện tích hình quạt tròn.

Lời giải chi tiết

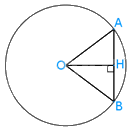
Giải bài tập 5.17 trang 98 SGK Toán 9 tập 1 - Kết nối tri thức 2

a) Vẽ bán kính OM của đường tròn, trên OM lấy điểm H sao cho OH = 2,5 cm. Kẻ đoạn thẳng AB vuông góc với OH tại H, cắt đường tròn tại A và B ta được dây cung AB cần vẽ.

b) Gọi H là trung điểm của AB.

Xét tam giác OAH và tam giác OBH có:

OA = OB = R

Cạnh OH chung

\(\widehat {OHA} = \widehat {OHB} = 90^\circ \)

suy ra \(\Delta OAH = \Delta OBH\) (cạnh huyền – cạnh góc vuông)

suy ra \(AH = BH\) (hai cạnh tương ứng), do đó \(AB = 2AH\)

Xét tam giác OAH vuông tại H có:

\(A{H^2} + O{H^2} = O{A^2}\) (định lý Pythagore)

hay \(A{H^2} = O{A^2} - O{H^2} = {5^2} - 2,{5^2} = 18,75\)

suy ra \(AH = \frac{5\sqrt 3}{2} \)(cm)

do đó \(AB = 2.\frac{5\sqrt 3}{2} = 5\sqrt 3 \approx 8,66\)(cm)

c) Xét tam giác OAH vuông tại H có:

\(\cos \widehat {AOH} = \frac{{OH}}{{OA}} = \frac{{2,5}}{5} = \frac{1}{2}\) suy ra \(\widehat {AOH} = 60^\circ \)

Mà: \(\Delta OAH = \Delta OBH\)

Do đó \(\widehat {BOH} = \widehat {AOH} = 60^\circ \)(hai góc tương ứng)

Suy ra \(\widehat {AOB} = \widehat {BOH} + \widehat {AOH} = 60^\circ + 60^\circ = 120^\circ \)

hay sđ\(\overset\frown{AB}=120{}^\circ \)

Độ dài cung AB là: \(\frac{{120}}{{180}}.\pi .5 = \frac{{10}}{3}\pi \)(cm)

d) Diện tích hình quạt tròn ứng với cung nhỏ AB là:

\(\frac{{{\rm{120}}}}{{{\rm{360}}}}{\rm{.\pi }}{\rm{.5^2 = }}\frac{{\rm{25\pi }}}{{{\rm{3}}}}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\)

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 5.17 trang 98 SGK Toán 9 tập 1 - Kết nối tri thức đặc sắc thuộc chuyên mục giải toán 9 trên nền tảng soạn toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 5.17 trang 98 SGK Toán 9 tập 1 - Kết nối tri thức: Hướng dẫn chi tiết

Bài tập 5.17 SGK Toán 9 tập 1 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến hàm số bậc nhất. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:

Định nghĩa hàm số bậc nhất: Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0.
Đồ thị hàm số bậc nhất: Đồ thị hàm số bậc nhất là một đường thẳng.
Cách xác định đường thẳng khi biết hai điểm: Nếu đường thẳng đi qua hai điểm A(x₁; y₁) và B(x₂; y₂) thì phương trình đường thẳng có dạng: (y - y₁) / (x - x₁) = (y₂ - y₁) / (x₂ - x₁).

Phân tích bài toán

Trước khi đi vào giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ các yếu tố quan trọng. Bài tập 5.17 thường đưa ra một tình huống thực tế, ví dụ như mối quan hệ giữa quãng đường đi được và thời gian, hoặc giữa số lượng sản phẩm và doanh thu. Nhiệm vụ của chúng ta là xây dựng hàm số bậc nhất mô tả mối quan hệ đó và sử dụng hàm số để trả lời các câu hỏi của bài toán.

Lời giải chi tiết bài tập 5.17

(Nội dung lời giải chi tiết bài tập 5.17 sẽ được trình bày ở đây, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Lời giải sẽ được chia thành các phần nhỏ để dễ theo dõi và hiểu.)

Ví dụ, nếu bài toán yêu cầu tìm hàm số biểu diễn chi phí vận chuyển hàng hóa theo quãng đường, chúng ta có thể thực hiện như sau:

Xác định các yếu tố: Gọi x là quãng đường vận chuyển (km), y là chi phí vận chuyển (đồng).
Tìm hai điểm thuộc đồ thị hàm số: Giả sử khi vận chuyển 10km, chi phí là 50.000 đồng, và khi vận chuyển 20km, chi phí là 100.000 đồng. Vậy ta có hai điểm A(10; 50.000) và B(20; 100.000).
Xác định phương trình đường thẳng: Sử dụng công thức xác định đường thẳng khi biết hai điểm, ta có: (y - 50.000) / (x - 10) = (100.000 - 50.000) / (20 - 10) = 5.000.
Giải phương trình để tìm hàm số: y - 50.000 = 5.000(x - 10) => y = 5.000x.
Kết luận: Hàm số biểu diễn chi phí vận chuyển hàng hóa theo quãng đường là y = 5.000x.

Các dạng bài tập tương tự

Ngoài bài tập 5.17, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Một số dạng bài tập thường gặp bao gồm:

Tìm hàm số khi biết đồ thị.
Xác định hệ số a và b của hàm số y = ax + b.
Giải các bài toán liên quan đến ứng dụng của hàm số bậc nhất trong kinh tế, vật lý, hóa học,...

Mẹo giải bài tập hàm số bậc nhất

Để giải tốt các bài tập về hàm số bậc nhất, các em học sinh cần:

Nắm vững định nghĩa và tính chất của hàm số bậc nhất.
Luyện tập thường xuyên các bài tập khác nhau.
Đọc kỹ đề bài và xác định rõ các yếu tố quan trọng.
Sử dụng các công thức và phương pháp giải phù hợp.

Tổng kết

Bài tập 5.17 trang 98 SGK Toán 9 tập 1 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và rèn luyện kỹ năng giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.