Giải bài tập 10.5 trang 100 SGK Toán 9 tập 2 - Kết nối tri thức

Bài tập 10.5 trang 100 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin làm bài tập.

Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp các em hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.

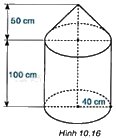
Một dụng cụ gồm một phần có dạng hình trụ và một phần có dạng hình nón với các kích thước như Hình 10.16. a) Tính thể tích của dụng cụ này. b) Tính diện tích mặt ngoài của dụng cụ (không tính đáy của dụng cụ).

Đề bài

Một dụng cụ gồm một phần có dạng hình trụ và một phần có dạng hình nón với các kích thước như Hình 10.16.

a) Tính thể tích của dụng cụ này.

b) Tính diện tích mặt ngoài của dụng cụ (không tính đáy của dụng cụ).

Giải bài tập 10.5 trang 100 SGK Toán 9 tập 2 - Kết nối tri thức 1

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 10.5 trang 100 SGK Toán 9 tập 2 - Kết nối tri thức 2

a) Thể tích của hình trụ có bán kính đáy R và chiều cao h là: V = S_đáy.h\( = \pi {R^2}h\).

Thể tích của hình nón bán kính r và chiều cao h là: \(V = \frac{1}{3}\pi {r^2}h\).

b) Diện tích xung quanh của hình trụ có bán kính đáy R và chiều cao h là: \({S_{xq}} = 2\pi Rh\).

Diện tích xung quanh của hình nón bán kính r và độ dài đường sinh l là: \({S_{xq}} = \pi rl\).

Lời giải chi tiết

Dụng cụ trên gồm:

+ Hình nón có chiều cao là 50cm, bán kính đáy bằng 40cm.

+ Hình trụ có chiều cao là 100cm, bán kính đáy bằng 40cm.

a) Thể tích của hình nón là:

\({V_1} = \frac{1}{3}\pi {.40^2}.50 = \frac{{80\;000\pi }}{3}\left( {c{m^3}} \right)\)

Thể tích của hình trụ là:

\({V_2} = \pi {.40^2}.100 = 160\;000\pi \left( {c{m^3}} \right)\)

Thể tích của dụng cụ là:

\(V = {V_1} + {V_2} = \frac{{80\;000\pi }}{3} + 160\;000\pi = \frac{{560\;000\pi }}{3}\left( {c{m^3}} \right)\)

b) Đường sinh của hình nón là:

\(\sqrt {{{50}^2} + {{40}^2}} = 10\sqrt {41} \left( {cm} \right)\).

Diện tích xung quanh của của hình nón là:

\({S_1} = \pi .10\sqrt {41} .40 = 400\sqrt {41} \pi \left( {c{m^2}} \right)\).

Diện tích xung quanh của của hình trụ là:

\({S_2} = 2\pi .40.100 = 8000\pi \left( {c{m^2}} \right)\).

Diện tích mặt ngoài của dụng cụ là:

\(S = {S_1} + {S_2} = 400\sqrt {41} \pi + 8000\pi = 400\pi \left( {\sqrt {41} + 20} \right)\left( {c{m^2}} \right)\)

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 10.5 trang 100 SGK Toán 9 tập 2 - Kết nối tri thức đặc sắc thuộc chuyên mục giải bài tập toán 9 trên nền tảng toán math. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 10.5 trang 100 SGK Toán 9 tập 2 - Kết nối tri thức: Hướng dẫn chi tiết

Bài tập 10.5 trang 100 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, tập trung vào việc ứng dụng kiến thức về hàm số bậc hai vào giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hàm số bậc hai, bao gồm:

Định nghĩa hàm số bậc hai: y = ax² + bx + c (a ≠ 0)
Đồ thị hàm số bậc hai (Parabol)
Các yếu tố của Parabol: đỉnh, trục đối xứng, giao điểm với trục hoành và trục tung
Tính chất của hàm số bậc hai: đồng biến, nghịch biến

Nội dung bài tập 10.5

Bài tập 10.5 thường yêu cầu học sinh:

Xác định hàm số bậc hai từ các thông tin cho trước.
Tìm tọa độ đỉnh của Parabol.
Xác định trục đối xứng của Parabol.
Tìm giao điểm của Parabol với trục hoành và trục tung.
Giải các bài toán thực tế liên quan đến hàm số bậc hai, ví dụ như tìm quỹ đạo của một vật được ném lên, tính diện tích của một hình chữ nhật có chiều dài và chiều rộng phụ thuộc vào một biến số.

Lời giải chi tiết bài tập 10.5 trang 100 SGK Toán 9 tập 2 - Kết nối tri thức

(Ở đây sẽ là lời giải chi tiết cho từng phần của bài tập 10.5. Ví dụ, nếu bài tập yêu cầu tìm tọa độ đỉnh của Parabol y = x² - 4x + 3, lời giải sẽ bao gồm các bước sau:)

Xác định hệ số a, b, c: a = 1, b = -4, c = 3
Tính hoành độ đỉnh: x_đỉnh = -b / 2a = -(-4) / (2 * 1) = 2
Tính tung độ đỉnh: y_đỉnh = a * x_đỉnh² + b * x_đỉnh + c = 1 * 2² - 4 * 2 + 3 = -1
Vậy tọa độ đỉnh của Parabol là (2; -1)

Phương pháp giải bài tập hàm số bậc hai hiệu quả

Để giải các bài tập về hàm số bậc hai một cách hiệu quả, học sinh nên:

Nắm vững các khái niệm cơ bản và công thức liên quan.
Luyện tập thường xuyên với nhiều dạng bài tập khác nhau.
Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị để kiểm tra kết quả.
Phân tích kỹ đề bài để xác định đúng yêu cầu và lựa chọn phương pháp giải phù hợp.
Kiểm tra lại kết quả sau khi giải xong để đảm bảo tính chính xác.

Ví dụ minh họa thêm

Xét hàm số y = -2x² + 8x - 5. Hãy tìm:

Tọa độ đỉnh của Parabol.
Trục đối xứng của Parabol.
Giao điểm của Parabol với trục tung.

(Lời giải chi tiết cho ví dụ này sẽ được trình bày tương tự như ví dụ trên)

Lưu ý quan trọng

Khi giải các bài tập về hàm số bậc hai, cần chú ý đến dấu của hệ số a. Nếu a > 0 thì Parabol có dạng chữ U, nếu a < 0 thì Parabol có dạng chữ ∩. Điều này sẽ giúp học sinh xác định được vị trí của Parabol và dự đoán được tính chất của hàm số.

Tổng kết

Bài tập 10.5 trang 100 SGK Toán 9 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết và phương pháp giải hiệu quả mà Giaitoan.edu.vn cung cấp, các em sẽ tự tin chinh phục bài tập này và đạt kết quả tốt trong môn Toán.