Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách giáo khoa Toán 9 Kết nối tri thức.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 2 trang 87, 88, 89. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Để bày bàn ăn cho nhiều người, các nhà hàng thường sử dụng bàn xoay có hình tròn và quay được quanh tâm của hình tròn. Đặt một chiếc cốc nhỏ ở vị trí điểm A trên bàn xoay hình tròn với tâm O sao cho điểm A khác điểm O. Khi quay bàn xoay thuận chiều kim đồng hồ (H.9.46) thì chiếc cốc di chuyển đến một vị trí mới là điểm B. Em hãy so sánh khoảng cách từ hai điểm A và B đến điểm O. Hai điểm A, B có cùng nằm trên một đường tròn tâm O hay không?
Video hướng dẫn giải
Trả lời câu hỏi Thử thách nhỏ 2 trang 89 SGK Toán 9 Kết nối tri thức
Hãy liệt kê 6 phép quay giữ nguyên một lục giác đều nội tiếp một đường tròn (O).
Phương pháp giải:
+ Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
+ Một phép quay được gọi là giữ nguyên một đa giác đều H nếu phép quay đó biến mỗi điểm của H thành một điểm của H.
Lời giải chi tiết:
6 phép quay giữ nguyên một lục giác đều nội tiếp một đường tròn (O) là: 6 phép quay thuận chiều kim đồng hồ góc \({\alpha ^o}\) tâm O với \({\alpha ^o}\) lần lượt nhận các giá trị \({60^o};{120^o};{180^o};{240^o};{300^o};{360^o}\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 87SGK Toán 9 Kết nối tri thức
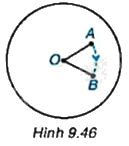
Để bày bàn ăn cho nhiều người, các nhà hàng thường sử dụng bàn xoay có hình tròn và quay được quanh tâm của hình tròn. Đặt một chiếc cốc nhỏ ở vị trí điểm A trên bàn xoay hình tròn với tâm O sao cho điểm A khác điểm O. Khi quay bàn xoay thuận chiều kim đồng hồ (H.9.46) thì chiếc cốc di chuyển đến một vị trí mới là điểm B.
Em hãy so sánh khoảng cách từ hai điểm A và B đến điểm O. Hai điểm A, B có cùng nằm trên một đường tròn tâm O hay không?
Phương pháp giải:
Khoảng cách từ hai điểm A và B đến O bằng nhau. Hai điểm A, B cùng nằm trên một đường tròn, có bán kính \(OA = OB\).
Lời giải chi tiết:
Khoảng cách từ hai điểm A và B đến O bằng nhau. Hai điểm A, B cùng nằm trên một đường tròn, có bán kính \(OA = OB\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 88 SGK Toán 9 Kết nối tri thức
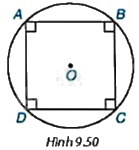
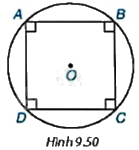
Cho hình vuông ABCD nội tiếp đường tròn (O) như Hình 9.50.
a) Phép quay thuận chiều \({90^o}\) tâm O biến các điểm A, B, C, D thành những điểm nào? Phép quay này có giữ nguyên hình vuông ABCD không?
b) Hãy liệt kê thêm ba phép quay khác với tâm O theo chiều kim đồng hồ giữ nguyên hình vuông ABCD.
Phương pháp giải:
+ Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
+ Một phép quay được gọi là giữ nguyên một đa giác đều H nếu phép quay đó biến mỗi điểm của H thành một điểm của H.
Lời giải chi tiết:
a) Phép quay thuận chiều \({90^o}\) tâm O biến các điểm A, B, C, D thành những điểm tương ứng B, C, D, A.
b) Ba phép quay khác với tâm O theo chiều kim đồng hồ giữ nguyên hình vuông ABCD là phép quay theo chiều \({\alpha ^o}\) tâm O với \({\alpha ^o}\) lần lượt nhận các giá trị \({180^o},{270^o},{360^o}\).
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 88SGK Toán 9 Kết nối tri thức
a) Phép quay ngược chiều \({180^o}\) tâm O biến điểm A thành điểm A’. Hỏi điểm A’ có đối xứng với điểm A qua O hay không?
b) Nếu phép quay thuận chiều \({\alpha ^o}\) tâm O biến điểm A thành điểm B thì phép quay ngược chiều \({\alpha ^o}\) tâm O biến điểm B thành điểm A hay không?
Phương pháp giải:
a) Chứng minh 3 điểm A, O, A’ thẳng hàng và \(OA = OA'\), suy ra điểm A’ có đối xứng với điểm A qua O.
b) Nếu phép quay thuận chiều \({\alpha ^o}\) tâm O biến điểm A thành điểm B thì phép quay ngược chiều \({\alpha ^o}\) tâm O biến điểm B thành điểm A.
Lời giải chi tiết:
a)

Phép quay ngược chiều \({180^o}\) tâm O biến điểm A thành điểm A’ thì \(OA = OA'\) và \(\widehat {A'OA} = {180^o}\). Do đó, 3 điểm A, O, A’ thẳng hàng và \(OA = OA'\). Suy ra, điểm A’ có đối xứng với điểm A qua O.
b) Nếu phép quay thuận chiều \({\alpha ^o}\) tâm O biến điểm A thành điểm B thì phép quay ngược chiều \({\alpha ^o}\) tâm O biến điểm B thành điểm A.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 87SGK Toán 9 Kết nối tri thức
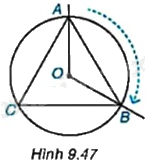
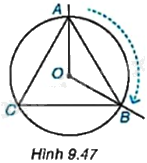
Trên bàn xoay tâm O, vẽ tam giác đều ABC nội tiếp một đường tròn (O) và hai tia OA, OB (H.9.47). Khi quay bàn xoay thuận chiều kim đồng hồ để tia OA di chuyển trùng với tia OB (ở vị trí ban đầu), điểm A có di chuyển đến điểm B không và sẽ di chuyển trên cung tròn nào của đường tròn (O)? Khi đó, điểm C sẽ di chuyển đến vị trí của điểm nào?
Phương pháp giải:
Khi quay bàn xoay thuận chiều kim đồng hồ để tia OA di chuyển trùng với tia OB (ở vị trí ban đầu), thì điểm A có di chuyển đến điểm B và sẽ di chuyển trên cung AB, điểm C di chuyển đến điểm A.
Lời giải chi tiết:
Khi quay bàn xoay thuận chiều kim đồng hồ để tia OA di chuyển trùng với tia OB (ở vị trí ban đầu), thì điểm A có di chuyển đến điểm B và sẽ di chuyển trên cung AB, điểm C di chuyển đến điểm A.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 87SGK Toán 9 Kết nối tri thức
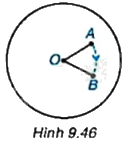
Để bày bàn ăn cho nhiều người, các nhà hàng thường sử dụng bàn xoay có hình tròn và quay được quanh tâm của hình tròn. Đặt một chiếc cốc nhỏ ở vị trí điểm A trên bàn xoay hình tròn với tâm O sao cho điểm A khác điểm O. Khi quay bàn xoay thuận chiều kim đồng hồ (H.9.46) thì chiếc cốc di chuyển đến một vị trí mới là điểm B.
Em hãy so sánh khoảng cách từ hai điểm A và B đến điểm O. Hai điểm A, B có cùng nằm trên một đường tròn tâm O hay không?
Phương pháp giải:
Khoảng cách từ hai điểm A và B đến O bằng nhau. Hai điểm A, B cùng nằm trên một đường tròn, có bán kính \(OA = OB\).
Lời giải chi tiết:
Khoảng cách từ hai điểm A và B đến O bằng nhau. Hai điểm A, B cùng nằm trên một đường tròn, có bán kính \(OA = OB\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 87SGK Toán 9 Kết nối tri thức
Trên bàn xoay tâm O, vẽ tam giác đều ABC nội tiếp một đường tròn (O) và hai tia OA, OB (H.9.47). Khi quay bàn xoay thuận chiều kim đồng hồ để tia OA di chuyển trùng với tia OB (ở vị trí ban đầu), điểm A có di chuyển đến điểm B không và sẽ di chuyển trên cung tròn nào của đường tròn (O)? Khi đó, điểm C sẽ di chuyển đến vị trí của điểm nào?
Phương pháp giải:
Khi quay bàn xoay thuận chiều kim đồng hồ để tia OA di chuyển trùng với tia OB (ở vị trí ban đầu), thì điểm A có di chuyển đến điểm B và sẽ di chuyển trên cung AB, điểm C di chuyển đến điểm A.
Lời giải chi tiết:
Khi quay bàn xoay thuận chiều kim đồng hồ để tia OA di chuyển trùng với tia OB (ở vị trí ban đầu), thì điểm A có di chuyển đến điểm B và sẽ di chuyển trên cung AB, điểm C di chuyển đến điểm A.
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 88SGK Toán 9 Kết nối tri thức
a) Phép quay ngược chiều \({180^o}\) tâm O biến điểm A thành điểm A’. Hỏi điểm A’ có đối xứng với điểm A qua O hay không?
b) Nếu phép quay thuận chiều \({\alpha ^o}\) tâm O biến điểm A thành điểm B thì phép quay ngược chiều \({\alpha ^o}\) tâm O biến điểm B thành điểm A hay không?
Phương pháp giải:
a) Chứng minh 3 điểm A, O, A’ thẳng hàng và \(OA = OA'\), suy ra điểm A’ có đối xứng với điểm A qua O.
b) Nếu phép quay thuận chiều \({\alpha ^o}\) tâm O biến điểm A thành điểm B thì phép quay ngược chiều \({\alpha ^o}\) tâm O biến điểm B thành điểm A.
Lời giải chi tiết:
a)

Phép quay ngược chiều \({180^o}\) tâm O biến điểm A thành điểm A’ thì \(OA = OA'\) và \(\widehat {A'OA} = {180^o}\). Do đó, 3 điểm A, O, A’ thẳng hàng và \(OA = OA'\). Suy ra, điểm A’ có đối xứng với điểm A qua O.
b) Nếu phép quay thuận chiều \({\alpha ^o}\) tâm O biến điểm A thành điểm B thì phép quay ngược chiều \({\alpha ^o}\) tâm O biến điểm B thành điểm A.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 88 SGK Toán 9 Kết nối tri thức
Cho hình vuông ABCD nội tiếp đường tròn (O) như Hình 9.50.
a) Phép quay thuận chiều \({90^o}\) tâm O biến các điểm A, B, C, D thành những điểm nào? Phép quay này có giữ nguyên hình vuông ABCD không?
b) Hãy liệt kê thêm ba phép quay khác với tâm O theo chiều kim đồng hồ giữ nguyên hình vuông ABCD.
Phương pháp giải:
+ Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
+ Một phép quay được gọi là giữ nguyên một đa giác đều H nếu phép quay đó biến mỗi điểm của H thành một điểm của H.
Lời giải chi tiết:
a) Phép quay thuận chiều \({90^o}\) tâm O biến các điểm A, B, C, D thành những điểm tương ứng B, C, D, A.
b) Ba phép quay khác với tâm O theo chiều kim đồng hồ giữ nguyên hình vuông ABCD là phép quay theo chiều \({\alpha ^o}\) tâm O với \({\alpha ^o}\) lần lượt nhận các giá trị \({180^o},{270^o},{360^o}\).
Video hướng dẫn giải
Trả lời câu hỏi Thử thách nhỏ 2 trang 89 SGK Toán 9 Kết nối tri thức
Hãy liệt kê 6 phép quay giữ nguyên một lục giác đều nội tiếp một đường tròn (O).
Phương pháp giải:
+ Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
+ Một phép quay được gọi là giữ nguyên một đa giác đều H nếu phép quay đó biến mỗi điểm của H thành một điểm của H.
Lời giải chi tiết:
6 phép quay giữ nguyên một lục giác đều nội tiếp một đường tròn (O) là: 6 phép quay thuận chiều kim đồng hồ góc \({\alpha ^o}\) tâm O với \({\alpha ^o}\) lần lượt nhận các giá trị \({60^o};{120^o};{180^o};{240^o};{300^o};{360^o}\).
Mục 2 của chương trình Toán 9 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc hai. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này yêu cầu học sinh xác định các hệ số a, b, c của hàm số bậc hai có dạng y = ax2 + bx + c. Để làm được bài tập này, học sinh cần nắm vững định nghĩa của hàm số bậc hai và biết cách nhận biết các hệ số a, b, c.
Ví dụ: Cho hàm số y = 2x2 - 3x + 1. Xác định các hệ số a, b, c.
Lời giải: a = 2, b = -3, c = 1.
Bài tập này yêu cầu học sinh tìm tập xác định của hàm số bậc hai. Tập xác định của hàm số bậc hai là tập hợp tất cả các giá trị của x sao cho biểu thức ax2 + bx + c có nghĩa.
Ví dụ: Tìm tập xác định của hàm số y = x2 + 1.
Lời giải: Tập xác định của hàm số là R (tập hợp tất cả các số thực).
Bài tập này yêu cầu học sinh vẽ đồ thị của hàm số bậc hai. Để vẽ đồ thị của hàm số bậc hai, học sinh cần xác định các điểm đặc biệt của đồ thị, như đỉnh, trục đối xứng, giao điểm với trục hoành và trục tung.
Ví dụ: Vẽ đồ thị của hàm số y = x2 - 4x + 3.
Lời giải:
Bài tập này yêu cầu học sinh tìm giá trị của x sao cho y có giá trị lớn nhất hoặc nhỏ nhất. Để làm được bài tập này, học sinh cần nắm vững tính chất của hàm số bậc hai và biết cách sử dụng công thức tính tọa độ đỉnh của đồ thị.
Ví dụ: Tìm giá trị của x sao cho y = -x2 + 2x + 1 có giá trị lớn nhất.
Lời giải: Vì a = -1 < 0 nên hàm số có giá trị lớn nhất tại đỉnh của đồ thị. xđỉnh = -b/2a = 1. Vậy giá trị của x sao cho y có giá trị lớn nhất là x = 1.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 2 trang 87, 88, 89 SGK Toán 9 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!