Bài tập 9.27 trang 89 SGK Toán 9 tập 2 thuộc chương trình Kết nối tri thức là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu cùng với phương pháp giải bài tập này.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trong quá trình học tập, cung cấp các giải pháp học toán online hiệu quả và chất lượng.
Cho hình thoi ABCD có (widehat A = {60^o}). Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.
Đề bài
Cho hình thoi ABCD có \(\widehat A = {60^o}\). Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Chứng minh tam giác ABD đều nên \(BD = AB = AD\).
+ Chứng minh \(MB = BN = PD = DQ = MQ = NP = \frac{{AB}}{2}\).
+ Chứng minh \(\widehat B = \widehat {BNP} = \widehat {NPD} = \widehat D = \widehat {DQM} = \widehat {QMB} = {120^o}\)
+ Suy ra MBNPDQ là lục giác đều.
Lời giải chi tiết
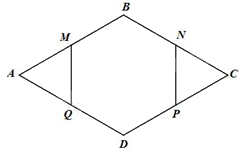
Vì ABCD là hình thoi nên \(AB = BC = CD = AD\).
Vì M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên \(MB = BN = NC = PC = PD = DQ = \frac{{AB}}{2}\) (1)
Tam giác ABD có: \(AB = AD\) nên tam giác ABD là tam giác cân tại A, mà \(\widehat A = {60^o}\) nên tam giác ABD đều. Do đó, \(AB = BD\).
Vì M, Q lần lượt là trung điểm của AB và AD (gt) nên MQ là đường trung bình của tam giác ABD. Do đó, \(MQ = \frac{1}{2}BD = \frac{1}{2}AB\) (2).
Vì N, P lần lượt là trung điểm của BC và CD (gt) nên NP là đường trung bình của tam giác CBD. Do đó, \(NP = \frac{1}{2}BD = \frac{1}{2}AB\) (3)
Từ (1), (2) và (3) ta có: \(MB = BN = PD = DQ = MQ = NP\) (*)
Vì ABCD là hình thoi nên \(\widehat {ABC} = \widehat {ADC};\widehat C = \widehat A = {60^o}\)
Ta có:
\(\widehat {ABC} + \widehat {ADC} + \widehat C + \widehat A = {360^o} \Rightarrow \widehat {ABC} = \widehat {ADC} = {360^o} - {2.60^o} = {120^o}\)
Tam giác NPC có: \(NC = PC\) nên tam giác NPC cân tại C. Mà \(\widehat C = {60^o}\) nên tam giác NPC đều.
Do đó, \(\widehat {CNP} = {60^o}\)
Ta có: \(\widehat {BNP} + \widehat {PNC} = {180^o}\) (hai góc kề bù) nên \(\widehat {BNP} = {120^o}\)
Chứng minh tương tự ta có:
\(\widehat {NPD} = \widehat {DQM} = \widehat {QMB} = {120^o}\)
Do đó: \(\widehat {ABC} = \widehat {ADC} = \widehat {BNP} = \widehat {NPD} = \widehat {DQM} = \widehat {QMB} = {120^o}\) (**)
Từ (*) và (**) ta có: MBNPDQ là lục giác đều.
Bài tập 9.27 SGK Toán 9 tập 2 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc xác định hàm số bậc nhất và ứng dụng vào việc tính toán các đại lượng liên quan.
Một người đi xe máy từ A đến B với vận tốc 40 km/h. Nếu vận tốc tăng thêm 5 km/h thì thời gian đi từ A đến B giảm đi 18 phút. Tính khoảng cách AB.
Để giải bài toán này, chúng ta cần sử dụng các kiến thức về hàm số bậc nhất, mối quan hệ giữa vận tốc, thời gian và quãng đường. Cụ thể:
Bước 1: Đặt ẩn số
Gọi quãng đường AB là x (km).
Bước 2: Biểu diễn thời gian đi từ A đến B trong hai trường hợp
Thời gian đi từ A đến B với vận tốc 40 km/h là: x/40 (giờ)
Thời gian đi từ A đến B với vận tốc 45 km/h là: x/45 (giờ)
Bước 3: Lập phương trình
Theo đề bài, thời gian đi từ A đến B giảm đi 18 phút khi vận tốc tăng thêm 5 km/h. Đổi 18 phút thành giờ: 18 phút = 18/60 = 0.3 giờ.
Phương trình: x/40 - x/45 = 0.3
Bước 4: Giải phương trình
Quy đồng mẫu số: (9x - 8x) / 360 = 0.3
x / 360 = 0.3
x = 0.3 x 360
x = 108
Bước 5: Kết luận
Vậy quãng đường AB là 108 km.
Để củng cố kiến thức về hàm số bậc nhất và ứng dụng vào giải bài toán thực tế, bạn có thể luyện tập thêm các bài tập tương tự trong SGK Toán 9 tập 2 Kết nối tri thức và các tài liệu tham khảo khác.
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp các giải pháp học tập toàn diện cho học sinh từ cấp tiểu học đến cấp trung học phổ thông. Chúng tôi cung cấp:
Hãy truy cập Giaitoan.edu.vn ngay hôm nay để khám phá các khóa học và tài liệu học tập hữu ích!
Hàm số bậc nhất được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, ví dụ như:
Bài tập 9.27 trang 89 SGK Toán 9 tập 2 Kết nối tri thức là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải bài tập và học tốt môn Toán.