Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2 - Kết nối tri thức. Bài tập 13 trang 129 là một trong những bài tập quan trọng giúp học sinh củng cố kiến thức về chủ đề đang học.
Chúng tôi hiểu rằng việc tự giải bài tập đôi khi gặp khó khăn, vì vậy đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải thích rõ ràng, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Cho tam giác ABC (left( {AB < AC} right)) ngoại tiếp đường tròn (I) với các tiếp điểm BC, CA, AB lần lượt là D, E, F. Gọi X và Y lần lượt là chân đường cao kẻ từ B và C xuống CI và BI. Chứng minh rằng: a) DBXF, DCYE là các tứ giác nội tiếp. b) Bốn điểm X, Y, E, F thẳng hàng.
Đề bài
Cho tam giác ABC \(\left( {AB < AC} \right)\) ngoại tiếp đường tròn (I) với các tiếp điểm BC, CA, AB lần lượt là D, E, F. Gọi X và Y lần lượt là chân đường cao kẻ từ B và C xuống CI và BI. Chứng minh rằng:
a) DBXF, DCYE là các tứ giác nội tiếp.
b) Bốn điểm X, Y, E, F thẳng hàng.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh tam giác IFB vuông tại F, tam giác BID vuông tại D, tam giác BXI vuông tại X nên 5 điểm I, B, D, F, X thuộc đường tròn đường kính BI. Do đó, tứ giác DBFX nội tiếp.
Chứng minh tương tự ta có tứ giác DCEY là tứ giác nội tiếp.
b) Chứng minh tứ giác XYCB nội tiếp nên \(\widehat {YXC} = \widehat {YBC}\)
+ Chứng minh \(\widehat {FXB} = \widehat {FDB}\).
+ Chứng minh BI là trung trực của DF. Suy ra, \(BI \bot FD\). Do đó, \(\widehat {YBC} + \widehat {FDB} = {90^o}\)
+ Chứng minh \(\widehat {FXB} + \widehat {YXC} = {90^o}\)
+ Chứng minh \(\widehat {FXY} = \widehat {FXB} + \widehat {YXC} + \widehat {BXC} = {180^o}\) nên 3 điểm F, X, Y thẳng hàng.
+ Chứng minh tương tự ta có: 3 điểm X, Y, E thẳng hàng.
Lời giải chi tiết
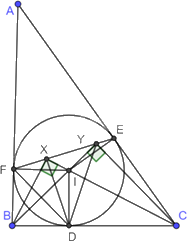
a) Vì ID, IE, IF là tiếp tuyến của đường tròn (I) nên \(IF \bot BF,ID \bot BC,IE \bot AC\)
Do đó, \(\widehat {IFB} = \widehat {IDB} = \widehat {IDC} = \widehat {IEC} = {90^o}\)
Suy ra, \(\Delta \)IFB vuông tại F, \(\Delta \)BID vuông tại D nên 4 điểm I, B, D, F thuộc đường tròn đường kính BI.
\(\Delta \)BXI vuông tại X nên X thuộc đường tròn đường kính BI.
Do đó, 5 điểm I, B, D, F, X thuộc đường tròn đường kính BI. Do đó, tứ giác DBFX nội tiếp.
Chứng minh tương tự ta có: tứ giác DCEY là tứ giác nội tiếp.
b) Vì \(\Delta \)BXC vuông tại X, \(\Delta \)BYC vuông tại Y nên 4 điểm B, X, Y, C thuộc đường tròn đường kính BC. Do đó, \(\widehat {YXC} = \widehat {YBC}\) (1) (góc nội tiếp cùng chắn cung YC).
Xét đường tròn đường kính BI có: \(\widehat {FXB} = \widehat {FDB}\) (2) (góc nội tiếp cùng chắn cung BF).
Vì BF và BD là tiếp tuyến của đường tròn (I) nên \(BF = BD\) nên B thuộc đường trung trực của DF.
Lại có: \(IF = ID\) (bán kính đường tròn (I)) nên I thuộc đường trung trực của DF.
Do đó, BI là trung trực của DF. Suy ra, \(BI \bot FD\). Do đó, \(\widehat {YBC} + \widehat {FDB} = {90^o}\) (3).
Từ (1), (2) và (3) ta có: \(\widehat {FXB} + \widehat {YXC} = {90^o}\)
Do đó, \(\widehat {FXY} = \widehat {FXB} + \widehat {YXC} + \widehat {BXC} = {90^o} + {90^o} = {180^o}\). Do đó, 3 điểm F, X, Y thẳng hàng.
Chứng minh tương tự ta có: 3 điểm X, Y, E thẳng hàng.
Vậy X, Y, E, F thẳng hàng.
Bài tập 13 trang 129 SGK Toán 9 tập 2 - Kết nối tri thức thuộc chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và định lý liên quan.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp bạn tập trung vào những thông tin cần thiết và tránh những sai sót không đáng có.
(Giả sử đề bài là: Cho tam giác ABC, điểm D nằm trên cạnh AB, điểm E nằm trên cạnh AC sao cho DE song song với BC. Biết AD = 4cm, DB = 6cm, AE = 5cm. Tính AC.)
Hướng dẫn giải:
Kết luận: AC = 12.5cm
Ngoài bài tập 13, trang 129, SGK Toán 9 tập 2 - Kết nối tri thức còn nhiều bài tập tương tự khác. Để giải quyết các bài tập này, bạn có thể áp dụng các phương pháp sau:
Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:
Bài tập 13 trang 129 SGK Toán 9 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về định lý Thales, tính chất đường trung bình của tam giác và tam giác đồng dạng. Bằng cách nắm vững các kiến thức này và áp dụng các phương pháp giải phù hợp, bạn có thể tự tin giải quyết các bài tập tương tự.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp bạn hiểu rõ hơn về bài tập 13 trang 129 SGK Toán 9 tập 2 - Kết nối tri thức và đạt kết quả tốt trong học tập.