Chào mừng bạn đến với bài học lý thuyết về căn bậc ba và căn thức bậc ba trong chương trình Toán 9 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về chủ đề này.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất, các phép toán và ứng dụng của căn bậc ba và căn thức bậc ba. Mục tiêu là giúp bạn hiểu rõ bản chất và có thể áp dụng linh hoạt vào giải các bài tập.
1. Căn bậc ba Khái niệm căn bậc ba của một số thực
1. Căn bậc ba
Khái niệm căn bậc ba của một số thực
Căn bậc ba của số thực a là số thực x thỏa mãn \({x^3} = a\). |
Chú ý:
- Mỗi số a đều có duy nhất một căn bậc ba.
- Căn bậc ba của số a được kí hiệu là \(\sqrt[3]{a}\), trong đó số 3 được gọi là chỉ số của căn.
Nhận xét: Từ định nghĩa căn bậc ba, ta có \({\left( {\sqrt[3]{a}} \right)^3} = \sqrt[3]{{{a^3}}} = a\) với mọi số thực a.
Ví dụ:
\(\sqrt[3]{{64}} = \sqrt[3]{{{4^3}}} = 4\);
\(\sqrt[3]{{ - 27}} = \sqrt[3]{{{{\left( { - 3} \right)}^3}}} = - 3\).
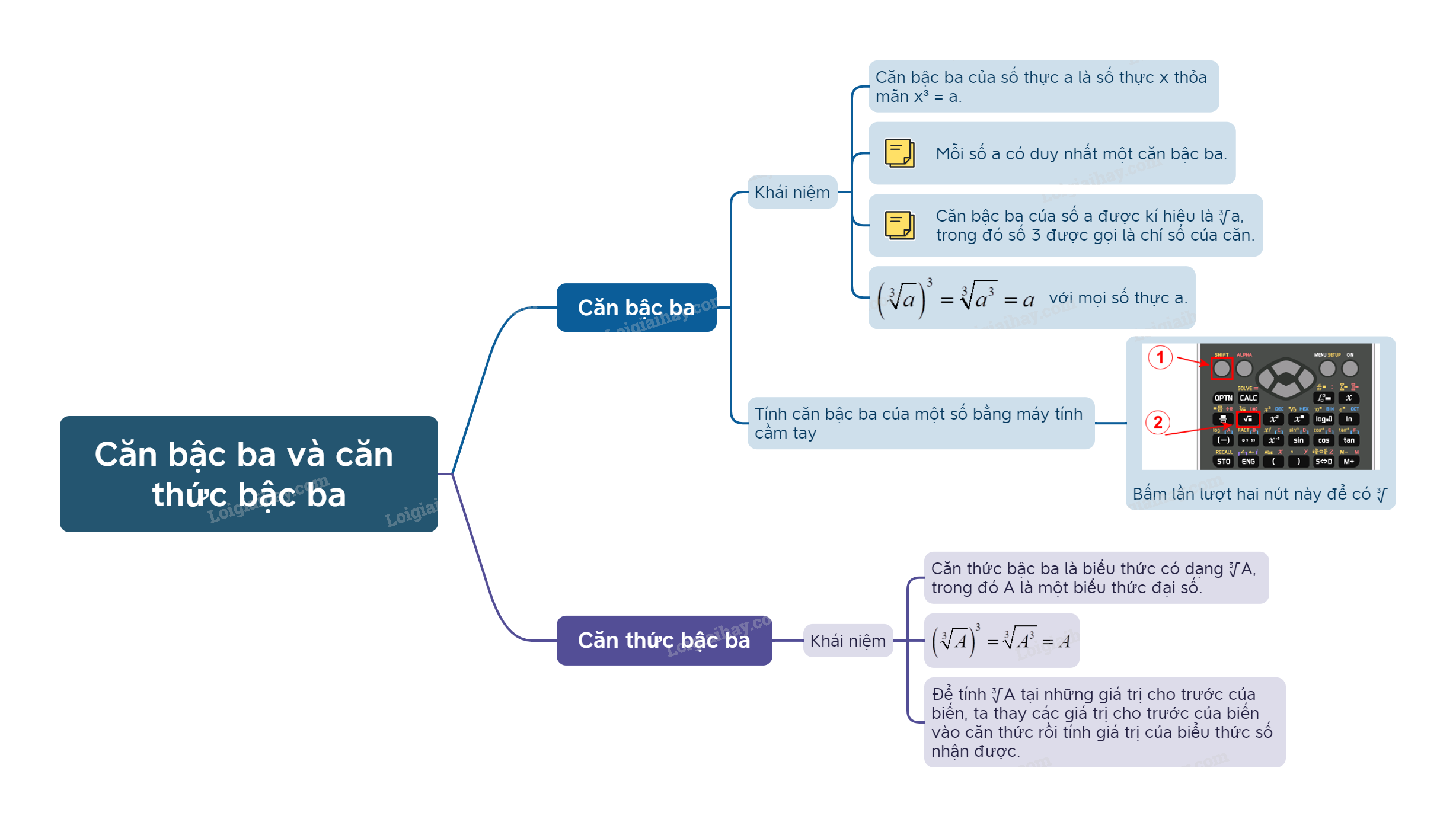
Tính căn bậc ba của một số bằng máy tính cầm tay
Ta có thể sử dụng loại MTCT thích hợp để tính căn bậc ba của một số.
Căn bậc ba là một khái niệm quan trọng trong toán học, đặc biệt là trong chương trình Toán 9. Nó là phép toán ngược của lũy thừa bậc ba. Để hiểu rõ hơn về căn bậc ba và căn thức bậc ba, chúng ta cần nắm vững các định nghĩa và tính chất cơ bản.
Căn bậc ba của một số thực a, ký hiệu là ∛a, là số thực x sao cho x3 = a. Nói cách khác, x là số mà khi nhân với chính nó ba lần sẽ cho ra a.
Ví dụ:
Căn thức bậc ba là biểu thức có dạng ∛A, trong đó A là một biểu thức đại số. Căn thức bậc ba cũng tuân theo các quy tắc về dấu và phép toán.
Căn bậc ba có một số tính chất quan trọng sau:
Chúng ta có thể thực hiện các phép toán cộng, trừ, nhân, chia với căn bậc ba. Tuy nhiên, cần lưu ý rằng chỉ có thể cộng hoặc trừ các căn bậc ba có cùng biểu thức bên trong căn.
Ví dụ:
Đôi khi, chúng ta cần khử mẫu của căn thức bậc ba để đơn giản biểu thức. Để làm điều này, chúng ta nhân cả tử và mẫu của căn thức với một biểu thức thích hợp sao cho mẫu trở thành một số lập phương hoàn chỉnh.
Ví dụ:
∛(1/2) = ∛(1/2 * 4/4) = ∛(4/8) = ∛4 / 2
Để so sánh hai căn bậc ba, chúng ta có thể nâng lũy thừa bậc ba cả hai số và so sánh kết quả. Hoặc, chúng ta có thể ước lượng giá trị của các căn bậc ba để so sánh.
Căn bậc ba và căn thức bậc ba có nhiều ứng dụng trong toán học và các lĩnh vực khác, chẳng hạn như:
Để củng cố kiến thức, hãy thử giải các bài tập sau:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết căn bậc ba và căn thức bậc ba Toán 9 Kết nối tri thức. Chúc bạn học tập tốt!