Bài tập 4.15 trang 80 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế liên quan đến việc xác định hàm số và ứng dụng của nó.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 4.15 trang 80 SGK Toán 9 tập 1 - Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết (HB = 3cm,HC = 6cm,widehat {HAC} = {60^0}.) Hãy tính độ dài các cạnh (làm tròn đến cm) , số đo các góc của tam giác ABC (làm tròn đến độ) .
Đề bài
Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết \(HB = 3cm,HC = 6cm,\widehat {HAC} = {60^0}.\) Hãy tính độ dài các cạnh (làm tròn đến cm) , số đo các góc của tam giác ABC (làm tròn đến độ) .
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Ta cần tính các cạnh AB, BC, CA
\(BC = BH + HC\); AC tính dựa vào tỉ số lượng giác của \(\widehat {HAC}\) (\(\sin \widehat {HAC}\) )
Cạnh AB tính thông qua định lý Pythagore trong tam giác vuông ABH, tuy nhiên ta cần tính được cạnh AH, tính cạnh AH thông qua tỉ số lượng giác của \(\widehat {HAC}\left( {\tan \widehat {HAC}} \right)\)
Lời giải chi tiết
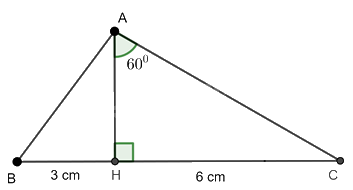
Cạnh \(BC = BH + HC = 3 + 6 = 9\) cm
Ta có:
\(\sin \widehat {HAC} = \frac{{HC}}{{AC}}\) hay \(\sin {60^0} = \frac{6}{{AC}}\) hay \(AC = \frac{6}{{\sin {{60}^0}}} = 4\sqrt 3 \approx 7\) cm
\(\tan \widehat {HAC} = \frac{{HC}}{{AH}}\) hay \(\tan {60^0} = \frac{6}{{AH}}\) nên \(AH = \frac{6}{{\tan {{60}^0}}} = 2\sqrt 3 \) cm
\(\widehat C = 90^\circ - 60^\circ = 30^\circ\)
Tam giác ABH vuông tại H nên ta có:
\(A{B^2} = A{H^2} + B{H^2} = {\left( {2\sqrt 3 } \right)^2} + {3^2} = 21\) hay \(AB = \sqrt {21} \approx 5\) cm (vì \(AB > 0\))
Ta có: \(tan B = \frac{AH}{BH} = \frac{2\sqrt 3}{3}\) suy ra \( \widehat B \approx 49^\circ\)
Áp dụng định lí tổng ba góc trong một tam giác, ta có:
\(\widehat {BAC} = 180^\circ - (\widehat B + \widehat C) = 180^\circ - (49^\circ + 30^\circ) = 101^\circ\)
Bài tập 4.15 trang 80 SGK Toán 9 tập 1 - Kết nối tri thức là một bài toán ứng dụng thực tế về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Nội dung bài tập 4.15:
Một người đi xe đạp từ A đến B với vận tốc 12km/h. Hỏi người đó đi hết bao lâu nếu quãng đường AB dài 36km?
Lời giải:
Gọi t là thời gian người đó đi từ A đến B (t tính bằng giờ).
Quãng đường AB dài 36km, vận tốc của người đi xe đạp là 12km/h. Ta có công thức:
Quãng đường = Vận tốc × Thời gian
36 = 12 × t
t = 36 / 12
t = 3
Vậy người đó đi hết 3 giờ để đi từ A đến B.
Phân tích bài giải:
Bài giải trên sử dụng công thức quãng đường = vận tốc × thời gian để tính thời gian người đi xe đạp đi từ A đến B. Đây là một ứng dụng đơn giản của hàm số bậc nhất, trong đó quãng đường là biến số phụ thuộc, vận tốc là hệ số góc và thời gian là biến số độc lập.
Mở rộng:
Nếu vận tốc của người đi xe đạp thay đổi, ví dụ như người đó đi nhanh hơn hoặc chậm hơn, thì thời gian đi từ A đến B cũng sẽ thay đổi. Trong trường hợp này, ta có thể sử dụng hàm số bậc nhất để mô tả mối quan hệ giữa vận tốc, thời gian và quãng đường.
Ví dụ, nếu vận tốc của người đi xe đạp là v (km/h), thì thời gian đi từ A đến B là t = 36/v (giờ).
Bài tập tương tự:
Kết luận:
Bài tập 4.15 trang 80 SGK Toán 9 tập 1 - Kết nối tri thức là một bài toán ứng dụng thực tế về hàm số bậc nhất. Việc giải bài tập này giúp học sinh hiểu rõ hơn về khái niệm hàm số bậc nhất và ứng dụng của nó trong việc giải quyết các bài toán thực tế.
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về bài tập 4.15 trang 80 SGK Toán 9 tập 1 - Kết nối tri thức và tự tin hơn trong việc học tập môn Toán.