Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2 - Kết nối tri thức. Bài tập 9 trang 128 là một trong những bài tập quan trọng giúp học sinh củng cố kiến thức về chủ đề đang học.
Chúng tôi cam kết mang đến cho bạn trải nghiệm học toán online tốt nhất với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giải bài tập khoa học.
Để đo khoảng cách giữa hai điểm A và B không tới được, một người đứng ở điểm H sao cho B ở giữa A và H rồi dịch chuyển đến điểm K sao cho KH vuông góc với AB tại H, (HK = aleft( m right)), ngắm nhìn A với (widehat {AKH} = alpha ), ngắm nhìn B với (widehat {BKH} = beta left( {alpha > beta } right)). a) Hãy biểu diễn AB theo (a,alpha ,beta ). b) Khi (a = 3m,alpha = {60^o},beta = {30^o}), hãy tính AB (làm tròn kết quả đến chữ số thập phân thứ ba của mét).
Đề bài
Để đo khoảng cách giữa hai điểm A và B không tới được, một người đứng ở điểm H sao cho B ở giữa A và H rồi dịch chuyển đến điểm K sao cho KH vuông góc với AB tại H, \(HK = a\left( m \right)\), ngắm nhìn A với \(\widehat {AKH} = \alpha \), ngắm nhìn B với \(\widehat {BKH} = \beta \left( {\alpha > \beta } \right)\).
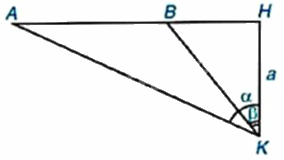
a) Hãy biểu diễn AB theo \(a,\alpha ,\beta \).
b) Khi \(a = 3m,\alpha = {60^o},\beta = {30^o}\), hãy tính AB (làm tròn kết quả đến chữ số thập phân thứ ba của mét).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Tam giác KBH vuông tại H nên \(BH = KH.\tan \widehat {HKB} = a.\tan \beta \).
+ Tam giác KAH vuông tại H nên \(AH = KH.\tan \widehat {HKA} = a.\tan \alpha \).
+ Do đó, \(AB = AH - BH = a\left( {\tan \alpha - \tan \beta } \right)\).
Lời giải chi tiết
a) \(\Delta \)KBH vuông tại H nên \(BH = KH.\tan \widehat {HKB} = a.\tan \beta \) (hệ thức giữa cạnh và góc trong tam giác vuông)
\(\Delta \)KAH vuông tại H nên \(AH = KH.\tan \widehat {HKA} = a.\tan \alpha \) (hệ thức giữa cạnh và góc trong tam giác vuông)
Do đó, \(AB = AH - BH = a\left( {\tan \alpha - \tan \beta } \right)\).
b) Với \(a = 3m,\alpha = {60^o},\beta = {30^o}\) ta có: \(AB = 3\left( {\tan {{60}^o} - \tan {{30}^o}} \right) = 3\left( {\sqrt 3 - \frac{{\sqrt 3 }}{3}} \right) = 2\sqrt 3 \approx 3,464\left( m \right)\).
Bài tập 9 trang 128 SGK Toán 9 tập 2 thuộc chương trình Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Để hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích từng bước một.
(Đề bài cụ thể của bài tập 9 sẽ được trình bày tại đây. Ví dụ: Cho hàm số y = ax2 + bx + c. Tìm a, b, c biết rằng đồ thị của hàm số đi qua các điểm A(0; 1), B(1; 2) và C(-1; 0).)
Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
(Lời giải chi tiết của bài tập 9 sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, giải thích rõ ràng và kết luận chính xác. Ví dụ:
)
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau xem xét một ví dụ minh họa:
(Ví dụ minh họa sẽ được trình bày tại đây, bao gồm đề bài, lời giải và giải thích chi tiết.)
Ngoài ra, chúng tôi cũng cung cấp một số bài tập tương tự để học sinh luyện tập:
Khi giải các bài tập về hàm số bậc hai, học sinh cần lưu ý những điều sau:
Hàm số bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài tập 9 trang 128 SGK Toán 9 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ có thể giải bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tốt!
| Tiêu chí | Mô tả |
|---|---|
| Kiến thức cần thiết | Định nghĩa hàm số bậc hai, cách xác định hệ số, giải hệ phương trình. |
| Phương pháp giải | Thay tọa độ điểm vào phương trình, giải hệ phương trình. |
| Lưu ý | Đọc kỹ đề, vận dụng kiến thức, kiểm tra kết quả. |