Giải bài tập 4.13 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức

Bài tập 4.13 trang 78 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Giaitoan.edu.vn sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

Chúng tôi luôn cố gắng cung cấp nội dung chính xác, cập nhật và hữu ích nhất cho học sinh. Hãy cùng giaitoan.edu.vn khám phá lời giải bài tập 4.13 này nhé!

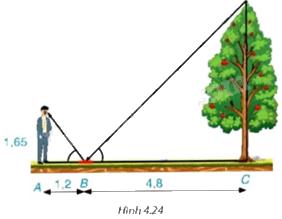
Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.24).

Đề bài

Giải bài tập 4.13 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức 1

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 4.13 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức 2

Góc tạo bởi đoạn thẳng nối từ mắt người đứng tới gương và đoạn thẳng AB bằng góc tạo bởi đoạn thẳng nối từ ngọn cây đến gương và đoạn thẳng BC.

Từ đó ta có thể sử dụng tam giác đồng dạng theo trường hợp góc góc để suy ra tỉ lệ các cạnh tương ứng, từ đó ta giải ra được chiều cao của cây, hoặc sử dụng tỉ số lượng giác của hai góc trên (\(\tan \alpha \) ) để tính chiều cao của cây.

Lời giải chi tiết

Gọi D là điểm tại mắt của người đứng, E là điểm trên đầu ngọn cây, ta có hình vẽ sau;

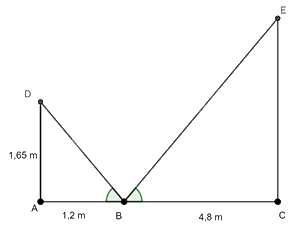
Giải bài tập 4.13 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức 3

Chiều cao của cây là đoạn EC

Ta có \(\tan \widehat {ABD} = \frac{{1,65}}{{1,2}} = \frac{{11}}{8}\) hay \(\tan \widehat {EBC} = \frac{{11}}{8}\) (do \(\widehat {ABC} = \widehat {DBC}\))

Mà \(\tan \widehat {EBC} = \frac{{EC}}{{BC}}\) suy ra \(\frac{{EC}}{{4,8}} = \frac{{11}}{8}\) hay \(EC = \frac{{11}}{8}.4,8 = 6,6\) m

Vậy chiều cao của cây là 6,6 m.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 4.13 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức đặc sắc thuộc chuyên mục sách bài tập toán 9 trên nền tảng học toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 4.13 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức: Phân tích và Lời giải chi tiết

Bài tập 4.13 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức là một bài toán ứng dụng thực tế, giúp học sinh củng cố kiến thức về hàm số bậc nhất và khả năng giải quyết vấn đề. Để giải bài tập này, chúng ta cần hiểu rõ các khái niệm cơ bản về hàm số bậc nhất, bao gồm:

Hàm số bậc nhất là gì? Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0.
Đồ thị của hàm số bậc nhất: Đồ thị của hàm số bậc nhất là một đường thẳng.
Cách xác định đường thẳng khi biết hai điểm: Nếu biết hai điểm thuộc đường thẳng, ta có thể xác định được phương trình của đường thẳng đó.

Nội dung bài tập 4.13: Bài tập yêu cầu xác định hàm số bậc nhất đi qua hai điểm cho trước. Đây là một dạng bài tập quen thuộc, nhưng đòi hỏi học sinh phải nắm vững các bước thực hiện.

Các bước giải bài tập 4.13 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức

Bước 1: Xác định tọa độ của hai điểm cho trước.
Bước 2: Thay tọa độ của hai điểm vào phương trình y = ax + b để tạo thành hệ phương trình.
Bước 3: Giải hệ phương trình để tìm ra giá trị của a và b.
Bước 4: Thay giá trị của a và b vào phương trình y = ax + b để có được phương trình hàm số bậc nhất cần tìm.

Ví dụ minh họa giải bài tập 4.13 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức

Giả sử bài tập yêu cầu tìm hàm số bậc nhất đi qua hai điểm A(1; 2) và B(3; 8). Ta thực hiện các bước sau:

Thay tọa độ điểm A(1; 2) vào phương trình y = ax + b, ta được: 2 = a(1) + b => a + b = 2 (1)
Thay tọa độ điểm B(3; 8) vào phương trình y = ax + b, ta được: 8 = a(3) + b => 3a + b = 8 (2)
Giải hệ phương trình (1) và (2):

Lấy phương trình (2) trừ phương trình (1), ta được: (3a + b) - (a + b) = 8 - 2 => 2a = 6 => a = 3
Thay a = 3 vào phương trình (1), ta được: 3 + b = 2 => b = -1

Vậy, hàm số bậc nhất cần tìm là y = 3x - 1.

Lưu ý khi giải bài tập 4.13 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức

Đảm bảo chính xác tọa độ của hai điểm cho trước.
Giải hệ phương trình một cách cẩn thận để tránh sai sót.
Kiểm tra lại kết quả bằng cách thay tọa độ của hai điểm vào phương trình hàm số vừa tìm được.

Bài tập tương tự và luyện tập

Để củng cố kiến thức về hàm số bậc nhất và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo các bài tập tương tự sau:

Tìm hàm số bậc nhất đi qua hai điểm C(-2; 1) và D(1; 4).
Tìm hàm số bậc nhất có đồ thị song song với đường thẳng y = 2x + 3 và đi qua điểm E(0; -1).

Giaitoan.edu.vn hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin giải quyết bài tập 4.13 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức và đạt kết quả tốt trong môn Toán.

Chúc các em học tập tốt!