Bài tập 9.43 trang 92 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trong quá trình học tập, cung cấp các tài liệu học tập chất lượng, đáp án nhanh chóng và chính xác.
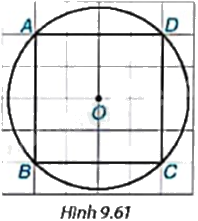
a) Phép quay thuận chiều ({45^o}) tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’ (H.9.61). Hãy vẽ tứ giác A’B’C’D’. b) Phép quay trong câu a biến các điểm A’, B’, C’, D’ thành những điểm nào?
Đề bài
a) Phép quay thuận chiều \({45^o}\) tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’ (H.9.61). Hãy vẽ tứ giác A’B’C’D’.
b) Phép quay trong câu a biến các điểm A’, B’, C’, D’ thành những điểm nào?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
+ Một phép quay được gọi là giữ nguyên một đa giác đều H nếu phép quay đó biến mỗi điểm của H thành một điểm của H.
Lời giải chi tiết
a) Tứ giác A’B’C’D’ được thể hiện như hình vẽ sau:
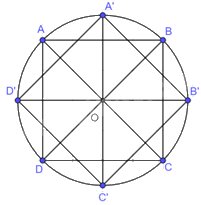
b) Phép quay thuận chiều \({45^o}\) tâm O biến các điểm A’, B’, C’, D’ lần lượt thành các điểm B, C, D, A.
Bài tập 9.43 trang 92 SGK Toán 9 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Nội dung bài tập 9.43: (Giả sử bài tập có nội dung cụ thể về một tình huống thực tế, ví dụ: Một quả bóng được ném lên từ mặt đất với vận tốc ban đầu là 15m/s. Hãy xác định độ cao lớn nhất mà quả bóng đạt được.)
Ví dụ minh họa:
Giả sử hàm số biểu diễn độ cao của quả bóng theo thời gian là: h(t) = -5t2 + 15t. (Trong đó: h(t) là độ cao của quả bóng tại thời điểm t, t là thời gian tính bằng giây).
Để tìm độ cao lớn nhất mà quả bóng đạt được, ta thực hiện các bước sau:
Các bài tập tương tự:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 9 tập 2 và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.
Giaitoan.edu.vn hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ hiểu rõ cách giải bài tập 9.43 trang 92 SGK Toán 9 tập 2 - Kết nối tri thức và đạt kết quả tốt trong học tập.
| Công thức | Mô tả |
|---|---|
| x = -b / 2a | Hoành độ đỉnh của parabol |
| y = ax2 + bx + c | Dạng tổng quát của hàm số bậc hai |