Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 93, 94 sách giáo khoa Toán 9 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án đầy đủ, kèm theo các bước giải chi tiết, giúp các em học sinh có thể tự học tại nhà hoặc ôn tập kiến thức một cách hiệu quả.
Em hãy tìm một số hình ảnh của hình quạt tròn và hình vành khuyên trong thực tế
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 93 SGK Toán 9 Kết nối tri thức
Biết rằng hai hình quạt tròn ứng với hai cung bằng nhau trên một đường tròn thì có diện tích bằng nhau và diện tích quạt tròn tỉ lệ với số đo của cung tương ứng với nó. Hãy thiết lập công thức tính diện tích hình quạt tròn bán kính R với cung \(n^\circ \) bằng cách thực hiện từng bước sau:
a) Tính diện tích hình quạt tròn ứng với cung \(1^\circ .\)
b) Tính diện tích hình quạt tròn ứng với cung \(n^\circ .\)
Phương pháp giải:
Đường tròn là cung có số đo bằng \(360^\circ \) và có diện bằng \(\pi {R^2}.\) Lấy diện tích hình tròn chia cho 360, ta được diện tích hình quạt tròn ứng với cung \(1^\circ .\) Sau đó nhân với n, ta được diện tích hình quạt tròn ứng với cung \(n^\circ .\)
Lời giải chi tiết:
a) Đường tròn là cung có số đo bằng \(360^\circ \) và có độ dài bằng \(\pi {R^2}.\)
Suy ra diện tích hình quạt tròn ứng với cung \(1^\circ \)là: \(\frac{{\pi {R^2}}}{{360}}\)
b) Diện tích hình quạt tròn ứng với của cung \(n^\circ \) là: \(\frac{n}{{360}}.\pi {R^2}\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 93 SGK Toán 9 Kết nối tri thức
Thiết lập công thức tính diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là R và r (R > r).
Phương pháp giải:
Lần lượt tính diện tích hai hình tròn, hiệu diện tích của hai hình tròn đó chính bằng diện tích của hình vành khuyên.
Lời giải chi tiết:
Diện tích hình tròn bán kính R là: \(\pi {R^2}.\)
Diện tích hình tròn bán kính r là: \(\pi {r^2}.\)
Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là R và r (R > r) là:
\(\pi {R^2} - \pi {r^2} = \pi \left( {{R^2} - {r^2}} \right).\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 94 SGK Toán 9 Kết nối tri thức
Tính diện tích của hình quạt tròn đã vẽ trong Thực hành trên nếu bán kính của nó bằng 4cm.
Phương pháp giải:
Tính số đo cung tương ứng với hình quạt tròn đã vẽ, sau đó áp dụng công thức tính diện tích hình quạt tròn.
Lời giải chi tiết:
Hình quạt tròn ứng với cung có số đo là:
\(360^\circ .40\% = 144^\circ \)
Diện tích hình quạt tròn là:
\(S = \frac{{\rm{n}}}{{360}}.{\rm{\pi }}{{\rm{R}}^2} = \frac{{144}}{{360}}.{\rm{\pi }}{.4^2} = 6,4{\rm{\pi }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành trang 94 SGK Toán 9 Kết nối tri thức
Trở lại tình huống mở đầu. Hãy vẽ (tô màu) hình quạt tròn theo hướng dẫn sau:
- Vẽ đường tròn tâm O (với bán kính tùy chọn).
- Hình quạt tròn cần vẽ ứng với cung có số đo bằng 40% của 3600. Tính số đo của cung cần vẽ.
- Vẽ góc ở tâm có số đo tìm được và tô màu hình quạt tròn tương ứng.
Phương pháp giải:
Tình huống mở đầu:
Số người trên một địa bàn đã được tiêm 4 mũi phòng dịch Covid-19 đạt 40% trong tổng số các đối tượng cần được tiêm. Để hoàn thành một biểu đồ hình quạt tròn, Trang cần vẽ hình quạt tròn biểu thị số liệu 40%. Em có thể giúp bạn Trang được không?
Qua các bước gợi ý ở đề bài phần thực hành ta có thể vẽ được biểu đồ quạt cho bạn Trang
Lời giải chi tiết:
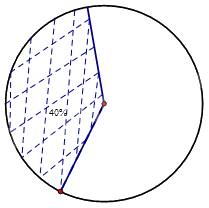
Vẽ đường tròn bánh kính bất kì, lấy 1 bán kính làm mốc.
40% của 3600 là:\(360^\circ .40\% = 144^\circ \)
Từ bán kính làm gốc ta đo góc 144 độ, nối từ tâm đến điểm đạt tại 144 độ, ta được phần biểu đồ cần vẽ ứng với 40%
Tô màu phần vừa biểu diễn ta được biểu đồ hình quạt tròn.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 94 SGK Toán 9 Kết nối tri thức
Một tấm bìa tạo bởi năm đường tròn đồng tâm lần lượt có bán kính là 5 cm, 10 cm, 15 cm, 20 cm và 30 cm (H.5.17). Giả thiết rằng người ném phi tiêu một cách ngẫu nhiên và luôn trúng bia. Tính xác suất ném trúng vòng 8 (hình vành khuyên nằm giữa đường tròn thứ hai và thứ ba), biết rằng xác xuất cần tìm bằng tỉ số giữa diện tích của hình vành khuyên tương ứng với diện tích của hình tròn lớn nhất.
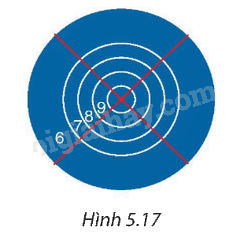
Phương pháp giải:
- Tính diện tích của vòng 8, diện tích của hình tròn lớn nhất.
- Xác xuất ném trúng vòng 8 = Diện tích vòng 8 : Diện tích hình tròn lớn nhất.
Lời giải chi tiết:
Diện tích của vòng 8 là: \(\pi \left( {{{15}^2} - {{10}^2}} \right) = 125\pi \,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Diện tích hình tròn lớn nhất là: \(\pi {.30^2} = 900\pi \,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Xác suất ném trúng vòng 8 là: \(\frac{{125\pi }}{{900\pi }} = \frac{5}{{36}}\)
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 93 SGK Toán 9 Kết nối tri thức
Em hãy tìm một số hình ảnh của hình quạt tròn và hình vành khuyên trong thực tế
Phương pháp giải:
Hình quạt tròn là phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai đầu mút của cung đó
Hình vành khuyên (còn gọi là hình vành khăn) là phần nằm giữa hai đường tròn có cùng tâm và bán kính khác nhau
Lời giải chi tiết:
Một số hình ảnh của quạt tròn trong thực tế: Bánh pizza, bánh phô mai con bò cười, quạt gấp,….

Một số hình ảnh của hình vành khuyên: Mũ rơm, đèn thả trần, viền của loa,…

Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 93 SGK Toán 9 Kết nối tri thức
Em hãy tìm một số hình ảnh của hình quạt tròn và hình vành khuyên trong thực tế
Phương pháp giải:
Hình quạt tròn là phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai đầu mút của cung đó
Hình vành khuyên (còn gọi là hình vành khăn) là phần nằm giữa hai đường tròn có cùng tâm và bán kính khác nhau
Lời giải chi tiết:
Một số hình ảnh của quạt tròn trong thực tế: Bánh pizza, bánh phô mai con bò cười, quạt gấp,….

Một số hình ảnh của hình vành khuyên: Mũ rơm, đèn thả trần, viền của loa,…

Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 93 SGK Toán 9 Kết nối tri thức
Biết rằng hai hình quạt tròn ứng với hai cung bằng nhau trên một đường tròn thì có diện tích bằng nhau và diện tích quạt tròn tỉ lệ với số đo của cung tương ứng với nó. Hãy thiết lập công thức tính diện tích hình quạt tròn bán kính R với cung \(n^\circ \) bằng cách thực hiện từng bước sau:
a) Tính diện tích hình quạt tròn ứng với cung \(1^\circ .\)
b) Tính diện tích hình quạt tròn ứng với cung \(n^\circ .\)
Phương pháp giải:
Đường tròn là cung có số đo bằng \(360^\circ \) và có diện bằng \(\pi {R^2}.\) Lấy diện tích hình tròn chia cho 360, ta được diện tích hình quạt tròn ứng với cung \(1^\circ .\) Sau đó nhân với n, ta được diện tích hình quạt tròn ứng với cung \(n^\circ .\)
Lời giải chi tiết:
a) Đường tròn là cung có số đo bằng \(360^\circ \) và có độ dài bằng \(\pi {R^2}.\)
Suy ra diện tích hình quạt tròn ứng với cung \(1^\circ \)là: \(\frac{{\pi {R^2}}}{{360}}\)
b) Diện tích hình quạt tròn ứng với của cung \(n^\circ \) là: \(\frac{n}{{360}}.\pi {R^2}\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 93 SGK Toán 9 Kết nối tri thức
Thiết lập công thức tính diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là R và r (R > r).
Phương pháp giải:
Lần lượt tính diện tích hai hình tròn, hiệu diện tích của hai hình tròn đó chính bằng diện tích của hình vành khuyên.
Lời giải chi tiết:
Diện tích hình tròn bán kính R là: \(\pi {R^2}.\)
Diện tích hình tròn bán kính r là: \(\pi {r^2}.\)
Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là R và r (R > r) là:
\(\pi {R^2} - \pi {r^2} = \pi \left( {{R^2} - {r^2}} \right).\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành trang 94 SGK Toán 9 Kết nối tri thức
Trở lại tình huống mở đầu. Hãy vẽ (tô màu) hình quạt tròn theo hướng dẫn sau:
- Vẽ đường tròn tâm O (với bán kính tùy chọn).
- Hình quạt tròn cần vẽ ứng với cung có số đo bằng 40% của 3600. Tính số đo của cung cần vẽ.
- Vẽ góc ở tâm có số đo tìm được và tô màu hình quạt tròn tương ứng.
Phương pháp giải:
Tình huống mở đầu:
Số người trên một địa bàn đã được tiêm 4 mũi phòng dịch Covid-19 đạt 40% trong tổng số các đối tượng cần được tiêm. Để hoàn thành một biểu đồ hình quạt tròn, Trang cần vẽ hình quạt tròn biểu thị số liệu 40%. Em có thể giúp bạn Trang được không?
Qua các bước gợi ý ở đề bài phần thực hành ta có thể vẽ được biểu đồ quạt cho bạn Trang
Lời giải chi tiết:
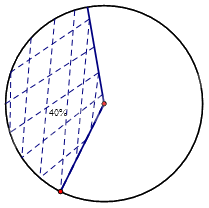
Vẽ đường tròn bánh kính bất kì, lấy 1 bán kính làm mốc.
40% của 3600 là:\(360^\circ .40\% = 144^\circ \)
Từ bán kính làm gốc ta đo góc 144 độ, nối từ tâm đến điểm đạt tại 144 độ, ta được phần biểu đồ cần vẽ ứng với 40%
Tô màu phần vừa biểu diễn ta được biểu đồ hình quạt tròn.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 94 SGK Toán 9 Kết nối tri thức
Tính diện tích của hình quạt tròn đã vẽ trong Thực hành trên nếu bán kính của nó bằng 4cm.
Phương pháp giải:
Tính số đo cung tương ứng với hình quạt tròn đã vẽ, sau đó áp dụng công thức tính diện tích hình quạt tròn.
Lời giải chi tiết:
Hình quạt tròn ứng với cung có số đo là:
\(360^\circ .40\% = 144^\circ \)
Diện tích hình quạt tròn là:
\(S = \frac{{\rm{n}}}{{360}}.{\rm{\pi }}{{\rm{R}}^2} = \frac{{144}}{{360}}.{\rm{\pi }}{.4^2} = 6,4{\rm{\pi }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 94 SGK Toán 9 Kết nối tri thức
Một tấm bìa tạo bởi năm đường tròn đồng tâm lần lượt có bán kính là 5 cm, 10 cm, 15 cm, 20 cm và 30 cm (H.5.17). Giả thiết rằng người ném phi tiêu một cách ngẫu nhiên và luôn trúng bia. Tính xác suất ném trúng vòng 8 (hình vành khuyên nằm giữa đường tròn thứ hai và thứ ba), biết rằng xác xuất cần tìm bằng tỉ số giữa diện tích của hình vành khuyên tương ứng với diện tích của hình tròn lớn nhất.
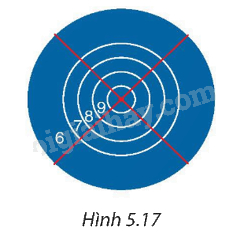
Phương pháp giải:
- Tính diện tích của vòng 8, diện tích của hình tròn lớn nhất.
- Xác xuất ném trúng vòng 8 = Diện tích vòng 8 : Diện tích hình tròn lớn nhất.
Lời giải chi tiết:
Diện tích của vòng 8 là: \(\pi \left( {{{15}^2} - {{10}^2}} \right) = 125\pi \,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Diện tích hình tròn lớn nhất là: \(\pi {.30^2} = 900\pi \,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Xác suất ném trúng vòng 8 là: \(\frac{{125\pi }}{{900\pi }} = \frac{5}{{36}}\)
Mục 2 trang 93, 94 SGK Toán 9 tập 1 - Kết nối tri thức tập trung vào việc ôn tập chương I: Hệ phương trình bậc nhất hai ẩn. Đây là một phần quan trọng trong chương trình Toán 9, giúp học sinh củng cố kiến thức về hệ phương trình, phương pháp giải và ứng dụng của chúng vào giải quyết các bài toán thực tế.
Mục 2 bao gồm các bài tập vận dụng kiến thức đã học để giải các hệ phương trình bậc nhất hai ẩn, tìm nghiệm của hệ phương trình, và xác định điều kiện để hệ phương trình có nghiệm duy nhất, vô nghiệm hoặc vô số nghiệm.
Bài tập này yêu cầu học sinh giải các hệ phương trình bậc nhất hai ẩn bằng các phương pháp đã học như phương pháp thế, phương pháp cộng đại số, hoặc phương pháp đồ thị.
Bài tập này yêu cầu học sinh tìm nghiệm của hệ phương trình bằng cách giải hệ phương trình và thay giá trị của x và y vào hệ phương trình để kiểm tra lại.
Bài tập này yêu cầu học sinh xác định điều kiện để hệ phương trình có nghiệm duy nhất, vô nghiệm hoặc vô số nghiệm bằng cách sử dụng các định lý và tính chất của hệ phương trình.
Khi giải hệ phương trình, cần lưu ý các điểm sau:
Hệ phương trình bậc nhất hai ẩn có nhiều ứng dụng trong thực tế, chẳng hạn như:
Để củng cố kiến thức và rèn luyện kỹ năng giải hệ phương trình, học sinh có thể tự giải thêm các bài tập nâng cao sau:
Hy vọng rằng bài viết này đã cung cấp cho học sinh những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 2 trang 93, 94 SGK Toán 9 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!