Giải bài tập 9.23 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức

Bài tập 9.23 trang 83 SGK Toán 9 tập 2 thuộc chương trình Kết nối tri thức là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng về hàm số bậc hai. Bài toán này thường yêu cầu học sinh xác định hệ số, tìm đỉnh của parabol, và vẽ đồ thị hàm số.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 9.23 trang 83 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.

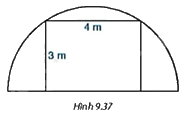
Người ta muốn dựng một khung cổng hình chữ nhật rộng 4m và cao 3m, bên ngoài khung cổng được bao bởi một khung thép dạng nửa đường tròn như Hình 9.37. Tính chiều dài của đoạn thép làm khung nửa đường tròn đó.

Đề bài

Giải bài tập 9.23 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức 1

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 9.23 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức 2

+ Gọi khung cổng hình chữ nhật là ABHG với \(AB = GH = 4m,AG = BH = 3m\). EF là đường kính của nửa đường tròn bao bởi khung cổng.

+ Gọi C là điểm đối xứng với B qua H, D là điểm đối xứng với A qua G.

+ Khi đó, ABCD là hình chữ nhật với \(AB = CD = 4m,AD = BC = 6m\).

+ Hình chữ nhật ABCD nội tiếp đường tròn đường kính AC bằng \(2\sqrt {13} m\), từ đó tính được chiều dài của đoạn thép làm nửa đường tròn là nửa chu vi của hình tròn đường kính AC.

Lời giải chi tiết

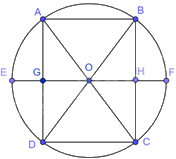
Giải bài tập 9.23 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức 3

Gọi khung cổng hình chữ nhật là ABHG với \(AB = GH = 4m,AG = BH = 3m\). EF là đường kính của nửa đường tròn bao bởi khung cổng.

Gọi C là điểm đối xứng với B qua H, D là điểm đối xứng với A qua G.

Khi đó, ABCD là hình chữ nhật với \(AB = CD = 4m,AD = BC = 6m\).

Suy ra, hình chữ nhật ABCD nội tiếp đường tròn tâm O, đường kính AC.

Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có:

\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{4^2} + {6^2}} = 2\sqrt {13} \left( m \right)\)

Do đó, chu vi đường tròn đường kính AC là:

\(P = AC.\pi = 2\sqrt {13} \pi \left( {m} \right)\)

Vậy chiều dài của đoạn khung thép làm nửa đường tròn đó là \(\frac{2\sqrt {13} \pi}{2} = \sqrt {13} \pi m\).

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 9.23 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức đặc sắc thuộc chuyên mục giải toán 9 trên nền tảng toán math. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 9.23 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức: Hướng dẫn chi tiết

Bài tập 9.23 SGK Toán 9 tập 2 yêu cầu chúng ta xét hàm số y = x² - 4x + 3. Để giải bài tập này một cách hiệu quả, chúng ta cần thực hiện các bước sau:

Xác định hệ số a, b, c: Trong hàm số y = x² - 4x + 3, ta có a = 1, b = -4, c = 3.
Tính delta (Δ): Δ = b² - 4ac = (-4)² - 4 * 1 * 3 = 16 - 12 = 4.
Xác định đỉnh của parabol: Vì Δ > 0, parabol có hai điểm phân biệt. Tọa độ đỉnh của parabol là I(-b/2a, -Δ/4a) = I(2, -1).
Xác định trục đối xứng: Trục đối xứng của parabol là đường thẳng x = -b/2a = x = 2.
Xác định giao điểm với trục Oy: Giao điểm với trục Oy là điểm có hoành độ x = 0. Thay x = 0 vào hàm số, ta được y = 3. Vậy giao điểm là A(0, 3).
Xác định giao điểm với trục Ox: Giao điểm với trục Ox là nghiệm của phương trình x² - 4x + 3 = 0. Giải phương trình này, ta được x₁ = 1 và x₂ = 3. Vậy giao điểm là B(1, 0) và C(3, 0).
Vẽ đồ thị hàm số: Dựa vào các thông tin đã tính toán, ta có thể vẽ đồ thị hàm số y = x² - 4x + 3.

Phân tích sâu hơn về hàm số y = x² - 4x + 3

Hàm số y = x² - 4x + 3 là một hàm số bậc hai có dạng tổng quát y = ax² + bx + c. Việc hiểu rõ các yếu tố như hệ số a, b, c, delta (Δ), đỉnh của parabol, trục đối xứng và giao điểm với các trục tọa độ là rất quan trọng để phân tích và vẽ đồ thị hàm số một cách chính xác.

Trong trường hợp này, vì a = 1 > 0, parabol có dạng mở lên trên. Đỉnh của parabol là điểm thấp nhất của đồ thị. Trục đối xứng chia parabol thành hai phần đối xứng nhau. Giao điểm với trục Oy cho biết vị trí của parabol trên trục Oy. Giao điểm với trục Ox cho biết nghiệm của phương trình bậc hai.

Ứng dụng của việc giải bài tập 9.23 trang 83 SGK Toán 9 tập 2

Việc giải bài tập 9.23 trang 83 SGK Toán 9 tập 2 không chỉ giúp học sinh nắm vững kiến thức về hàm số bậc hai mà còn có nhiều ứng dụng thực tế. Ví dụ, hàm số bậc hai được sử dụng để mô tả quỹ đạo của vật ném, diện tích của hình chữ nhật, và nhiều bài toán tối ưu hóa khác.

Ngoài ra, việc rèn luyện kỹ năng giải bài tập hàm số bậc hai còn giúp học sinh phát triển tư duy logic, khả năng phân tích và giải quyết vấn đề. Đây là những kỹ năng rất quan trọng trong học tập và cuộc sống.

Các bài tập tương tự và lời khuyên

Bài tập 9.24 trang 83 SGK Toán 9 tập 2: Tìm các điểm thuộc đồ thị hàm số y = 2x² - 5x + 1.
Bài tập 9.25 trang 84 SGK Toán 9 tập 2: Xác định hệ số a của hàm số y = ax² + bx + c biết rằng đồ thị hàm số đi qua các điểm A(0; 1), B(1; 4), C(-1; 0).

Để học tốt môn Toán 9, các em học sinh nên:

Nắm vững kiến thức cơ bản về hàm số bậc hai.
Luyện tập thường xuyên các bài tập về hàm số bậc hai.
Tìm hiểu các ứng dụng thực tế của hàm số bậc hai.
Sử dụng các tài liệu học tập và công cụ hỗ trợ học tập trực tuyến.

Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về bài tập 9.23 trang 83 SGK Toán 9 tập 2 và có thể tự tin giải các bài tập tương tự.