Bài tập 5.23 trang 103 SGK Toán 9 tập 1 thuộc chương trình Kết nối tri thức là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng về hàm số bậc nhất và ứng dụng của nó. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu cùng với các kiến thức liên quan để bạn có thể tự tin giải quyết bài toán này.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trong quá trình học tập, cung cấp các tài liệu và lời giải bài tập Toán 9 chính xác, nhanh chóng và hiệu quả.
Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F. a) Chứng minh rằng chu vi của tam giác SEF bằng SA + SB. b) Giả sử M là giao điểm của đoạn SO với đường tròn (O). Chứng minh rằng SE = SF.
Đề bài
Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F.
a) Chứng minh rằng chu vi của tam giác SEF bằng SA + SB.
b) Giả sử M là giao điểm của đoạn SO với đường tròn (O). Chứng minh rằng SE = SF.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng tính chất của hai tiếp tuyến cắt nhau.
Lời giải chi tiết
a)
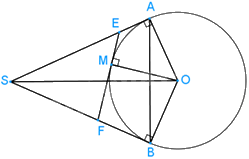
Hai tiếp tuyến EM và EA cắt nhau tại E nên EM = EA
Hai tiếp tuyến FM và EB cắt nhau tại F nên FM = FB
\(\begin{array}{*{20}{l}}{{C_{\Delta SEF}} = SE + SF + EF}\\{\; = SE + SF + EM + MF}\\{\; = SE + EA + SF + BF}\\{\; = SA + SB}\end{array}\)
b)
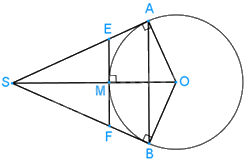
SA và SB là hai tiếp tuyến cắt nhau tại S nên SO là phân giác của góc \(\widehat {{\rm{ASB}}}\).
\( \Rightarrow \widehat {{\rm{OSA}}} = \widehat {{\rm{OSB}}}\) hay \(\widehat {{\rm{MSE}}} = \widehat {{\rm{MSF}}}\)
Xét tam giác SME và tam giác SMF có:
\(\widehat {{\rm{SME}}} = \widehat {{\rm{SMF}}} = 90^\circ \)
SM chung
\(\widehat {{\rm{MSE}}} = \widehat {{\rm{MSF}}}\)
\( \Rightarrow \Delta {\rm{SME}} = \Delta {\rm{SMF}}\) (g.c.g)
\( \Rightarrow {\rm{SE}} = {\rm{SF}}\) (hai cạnh tương ứng)
Bài tập 5.23 SGK Toán 9 tập 1 Kết nối tri thức yêu cầu chúng ta tìm hiểu về hàm số bậc nhất và cách xác định hệ số góc của đường thẳng.
Cho hàm số y = (m-1)x + 3. Tìm giá trị của m để hàm số đồng biến.
Để hàm số y = (m-1)x + 3 đồng biến, ta cần có hệ số góc (m-1) > 0.
Giải bất phương trình (m-1) > 0, ta được m > 1.
Vậy, để hàm số y = (m-1)x + 3 đồng biến thì m > 1.
Nếu m = 2, hàm số trở thành y = (2-1)x + 3 = x + 3. Đây là hàm số đồng biến vì hệ số góc bằng 1 > 0.
Khi giải các bài toán về hàm số bậc nhất, cần nắm vững định nghĩa về hàm số đồng biến, nghịch biến và hệ số góc. Đồng thời, cần chú ý đến điều kiện của các biến để đảm bảo lời giải chính xác.
Ngoài bài tập 5.23, các em có thể tham khảo thêm các bài tập khác trong SGK Toán 9 tập 1 Kết nối tri thức để củng cố kiến thức về hàm số bậc nhất. Các bài tập này sẽ giúp các em hiểu rõ hơn về ứng dụng của hàm số trong thực tế.
Bài tập 5.23 trang 103 SGK Toán 9 tập 1 Kết nối tri thức là một bài toán cơ bản về hàm số bậc nhất. Việc nắm vững kiến thức về hàm số đồng biến, nghịch biến và hệ số góc là rất quan trọng để giải quyết bài toán này một cách hiệu quả. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ tự tin hơn trong quá trình học tập môn Toán.
Giaitoan.edu.vn luôn cập nhật các lời giải bài tập Toán 9 mới nhất và chính xác nhất. Hãy truy cập website của chúng tôi để được hỗ trợ tốt nhất trong quá trình học tập.
| Hàm số | Hệ số góc | Tính chất |
|---|---|---|
| y = 2x + 1 | 2 | Đồng biến |
| y = -x + 3 | -1 | Nghịch biến |