Chào mừng bạn đến với bài học về Lý thuyết Bất đẳng thức và Tính chất trong chương trình Toán 9 Kết nối tri thức. Đây là một phần kiến thức quan trọng, nền tảng cho các bài toán nâng cao và các kỳ thi sắp tới.
Bài học này sẽ cung cấp cho bạn một cái nhìn tổng quan về bất đẳng thức, các tính chất cơ bản và cách áp dụng chúng vào giải toán. Chúng tôi sẽ đi sâu vào từng khái niệm, kèm theo ví dụ minh họa dễ hiểu.
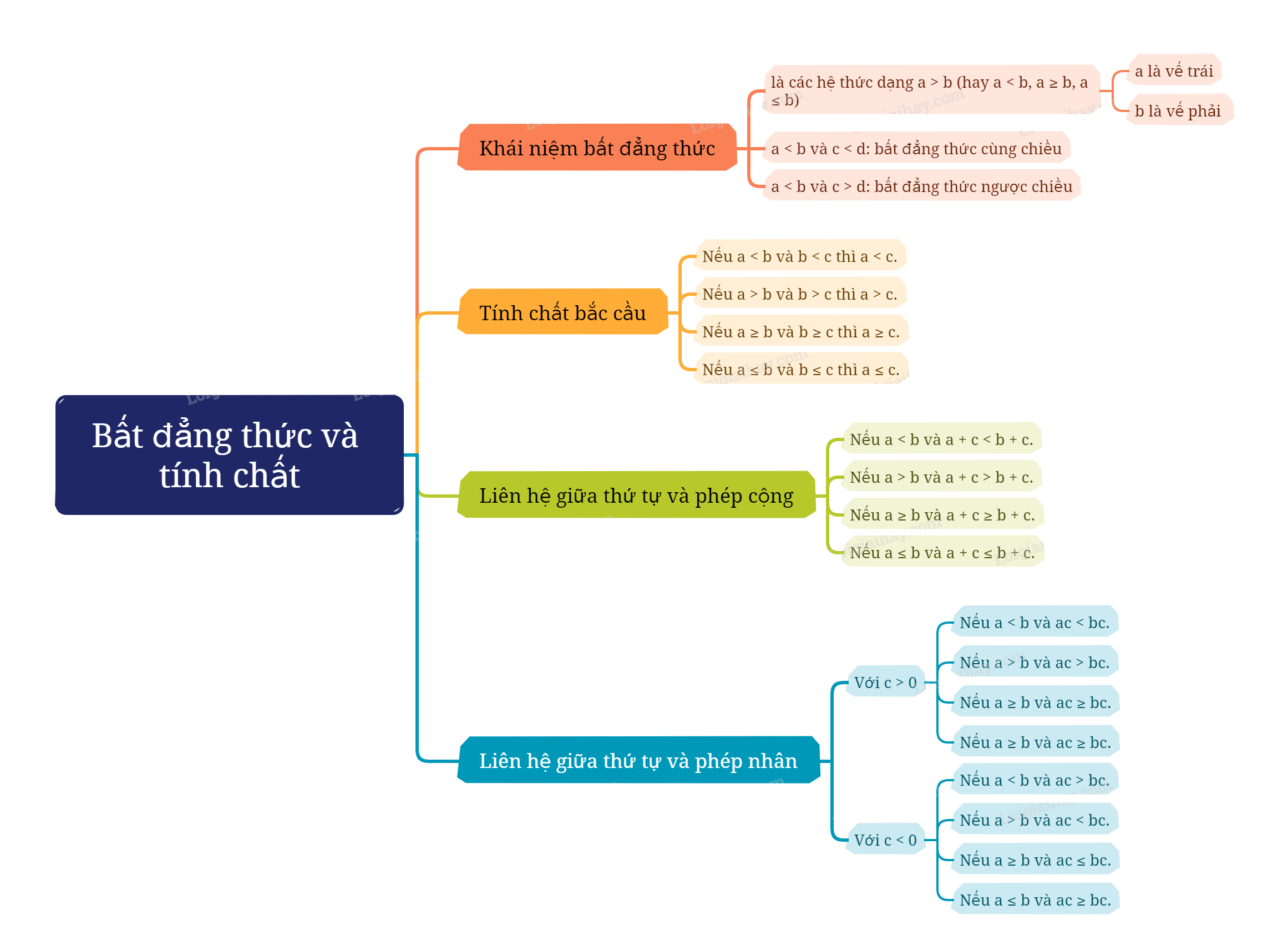
1. Bất đẳng thức Nhắc lại thứ tự trên tập số thực
1. Bất đẳng thức
Nhắc lại thứ tự trên tập số thực
Trên tập số thực, với hai số a và b có ba trường hợp sau:
a) Số a bằng số b, kí hiệu \(a = b\).
b) Số a lớn hơn số b, kí hiệu \(a > b\).
c) Số a nhỏ hơn số b, kí hiệu \(a < b\).
Khi biểu kiễn số thực trên trục số, điểm biểu diễn số bé hơn nằm trước điểm biểu diễn số lớn hơn.
Số a lớn hơn hoặc bằng số b, tức là \(a > b\) hoặc \(a = b\), kí hiệu là \(a \ge b\).
Số a nhỏ hơn hoặc bằng số b, tức là \(a < b\) hoặc \(a = b\), kí hiệu là \(a \le b\).
Khái niệm bất đẳng thức
Ta gọi hệ thức dạng \(a > b\) (hay \(a < b\), \(a \ge b\), \(a \le b\)) là bất đẳng thức và gọi a là vế trái, b là vế phải của bất đẳng thức. |
Chú ý:
Hai bất đẳng thức \(1 < 2\) và \( - 3 < - 2\) (hay \(6 > 3\) và \(8 > 5\)) được gọi là hai bất đẳng thức cùng chiều.
Hai bất đẳng thức \(1 < 2\) và \( - 2 > - 3\) (hay \(6 > 3\) và \(5 < 8\)) được gọi là hai bất đẳng thức ngược chiều.
Tính chất bắc cầu của bất đẳng thức
Nếu \(a < b\) và \(b < c\) thì \(a < c\). Nếu \(a > b\) và \(b > c\) thì \(a > c\). Nếu \(a \le b\) và \(b \le c\) thì \(a \le c\). Nếu \(a \ge b\) và \(b \ge c\) thì \(a \ge c\). |
Ví dụ: Vì \(\frac{{2024}}{{2023}} = 1 + \frac{1}{{2023}} > 1\) và \(\frac{{2021}}{{2022}} = 1 - \frac{1}{{2022}} < 1\) nên \(\frac{{2024}}{{2023}} > \frac{{2021}}{{2022}}\).
2. Liên hệ giữa thứ tự và phép cộng
Khi cộng cùng một số vào hai vế của một bất đẳng thức ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Nếu \(a < b\) thì \(a + c < b + c\). Nếu \(a > b\) thì \(a + c > b + c\). Nếu \(a \le b\) thì \(a + c \le b + c\). Nếu \(a \ge b\) thì \(a + c \ge b + c\). |
Ví dụ:Vì \(2023 < 2024\) nên \(2023 + \left( { - 19} \right) < 2024 + \left( { - 19} \right)\)
3. Liên hệ giữa thứ tự và phép nhân
- Khi nhân cả hai vế của một bất đẳng thức với cùng một số dương ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Với ba số a, b, c và c > 0, ta có: Nếu \(a < b\) thì \(ac < bc\). Nếu \(a > b\) thì \(ac > bc\). Nếu \(a \le b\) thì \(ac \le bc\). Nếu \(a \ge b\) thì \(ac \ge bc\). |
- Khi nhân cả hai vế của một bất đẳng thức với cùng một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho.
Với ba số a, b, c và c < 0, ta có: Nếu \(a < b\) thì \(ac > bc\). Nếu \(a > b\) thì \(ac < bc\). Nếu \(a \le b\) thì \(ac \ge bc\). Nếu \(a \ge b\) thì \(ac \le bc\). |
Ví dụ:
Vì \( - 7 < - 5\) và \(3 > 0\) nên \(3.\left( { - 7} \right) < 3.\left( { - 5} \right)\).
Vì \( - 7 < - 5\) và \( - 3 < 0\) nên \(\left( { - 3} \right).\left( { - 7} \right) > \left( { - 3} \right).\left( { - 5} \right)\).
Bất đẳng thức là một công cụ toán học mạnh mẽ, được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau. Trong chương trình Toán 9 Kết nối tri thức, việc nắm vững lý thuyết và tính chất của bất đẳng thức là vô cùng quan trọng.
Bất đẳng thức là một biểu thức toán học so sánh hai giá trị, sử dụng các ký hiệu: >, <, ≥, ≤. Ví dụ: a > b (a lớn hơn b), x < 5 (x nhỏ hơn 5).
Có một số tính chất cơ bản của bất đẳng thức mà bạn cần nắm vững:
Trong Toán 9, bạn sẽ thường gặp các loại bất đẳng thức sau:
Để giải bất đẳng thức bậc nhất một ẩn, bạn thực hiện các bước tương tự như giải phương trình bậc nhất, nhưng cần chú ý đến việc đổi chiều bất đẳng thức khi nhân hoặc chia hai vế với một số âm.
Ví dụ: Giải bất đẳng thức 2x + 3 > 5
Vậy nghiệm của bất đẳng thức là x > 1.
Để giải bất đẳng thức bậc hai một ẩn, bạn cần tìm nghiệm của phương trình bậc hai tương ứng, sau đó xét dấu của tam thức bậc hai để xác định tập nghiệm của bất đẳng thức.
Ví dụ: Giải bất đẳng thức x2 - 4x + 3 < 0
Vậy nghiệm của bất đẳng thức là 1 < x < 3.
Bất đẳng thức có nhiều ứng dụng trong thực tế, ví dụ như:
Để củng cố kiến thức, bạn hãy thử giải các bài tập sau:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về Lý thuyết Bất đẳng thức và Tính chất trong chương trình Toán 9 Kết nối tri thức. Chúc bạn học tốt!