Bài tập 5.39 trang 113 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Đây là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 5.39 này, giúp các em học sinh hiểu rõ phương pháp giải và tự tin hơn trong các bài kiểm tra.
Cho tam giác vuông ABC (A vuông). Vẽ hai đường tròn (B; BA) và (C; CA) cắt nhau tại A và A’. Chứng minh rằng: a) BA và BA’ là hai tiếp tuyến cắt nhau của (C; CA). b) CA và CA’ là hai tiếp tuyến cắt nhau của (B; BA).
Đề bài
Cho tam giác vuông ABC (A vuông). Vẽ hai đường tròn (B; BA) và (C; CA) cắt nhau tại A và A’. Chứng minh rằng:
a) BA và BA’ là hai tiếp tuyến cắt nhau của (C; CA).
b) CA và CA’ là hai tiếp tuyến cắt nhau của (B; BA).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh \(\Delta {\rm{ABC}} = \Delta {\rm{A'BC}}\) từ đó suy ra \(\widehat {{\rm{BA'C}}} = \widehat {{\rm{BAC}}} = 90^\circ \).
Do đó BA và BA’ là hai tiếp tuyến cắt nhau của (C; CA).
b) Lần lượt chứng minh CA và CA’ là các tiếp tuyến của (B; BA).
Lời giải chi tiết
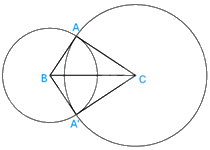
a) Xét tam giác ABC và tam giác A’BC có:
BA = BA’
BC chung
CA = CA’
Suy ra: \(\Delta {\rm{ABC}} = \Delta {\rm{A'BC}}\) (c.c.c)
Do đó: \(\widehat {{\rm{BA'C}}} = \widehat {{\rm{BAC}}} = 90^\circ \) (hai góc tương ứng)
Suy ra: \({\rm{CA'}} \bot {\rm{BA'}}\) tại A’ nên BA’ là tiếp tuyến của (C; CA)
Lại có: \({\rm{CA}} \bot {\rm{BA}}\) tại A nên BA là tiếp tuyến của (C; CA)
Vậy BA và BA’ là hai tiếp tuyến cắt nhau của (C; CA).
b) \({\rm{CA'}} \bot {\rm{BA'}}\) tại A’ nên CA’ là tiếp tuyến của (B; BA)
\({\rm{CA}} \bot {\rm{BA}}\) tại A nên CA là tiếp tuyến của (B; BA)
Vậy CA và CA’ là hai tiếp tuyến cắt nhau của (B; BA).
Bài tập 5.39 yêu cầu chúng ta xét hàm số bậc nhất y = (m-1)x + 3. Để hàm số này là hàm số bậc nhất, điều kiện cần và đủ là hệ số a (tức là m-1) phải khác 0. Do đó, m ≠ 1.
Phần a: Tìm giá trị của m để hàm số là hàm số bậc nhất.
Như đã phân tích ở trên, để y = (m-1)x + 3 là hàm số bậc nhất, ta cần m - 1 ≠ 0, suy ra m ≠ 1.
Phần b: Tìm giá trị của m để hàm số đồng biến.
Hàm số bậc nhất y = ax + b đồng biến khi a > 0. Trong trường hợp này, a = m - 1. Vậy, để hàm số y = (m-1)x + 3 đồng biến, ta cần m - 1 > 0, suy ra m > 1.
Phần c: Tìm giá trị của m để hàm số nghịch biến.
Hàm số bậc nhất y = ax + b nghịch biến khi a < 0. Trong trường hợp này, a = m - 1. Vậy, để hàm số y = (m-1)x + 3 nghịch biến, ta cần m - 1 < 0, suy ra m < 1.
Ví dụ minh họa:
Giả sử m = 2. Khi đó, hàm số trở thành y = (2-1)x + 3 = x + 3. Đây là hàm số bậc nhất và đồng biến vì hệ số của x là 1 > 0.
Giả sử m = 0. Khi đó, hàm số trở thành y = (0-1)x + 3 = -x + 3. Đây là hàm số bậc nhất và nghịch biến vì hệ số của x là -1 < 0.
Lưu ý quan trọng:
Mở rộng kiến thức:
Ngoài bài tập 5.39, các em học sinh có thể tham khảo thêm các bài tập khác trong SGK Toán 9 tập 1 - Kết nối tri thức để củng cố kiến thức về hàm số bậc nhất. Các em cũng có thể tìm kiếm các tài liệu học tập trực tuyến hoặc tham gia các khóa học toán online để nâng cao kỹ năng giải toán.
Tổng kết:
Bài tập 5.39 trang 113 SGK Toán 9 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ về hàm số bậc nhất. Bằng cách nắm vững kiến thức và rèn luyện kỹ năng giải toán, các em học sinh có thể tự tin hơn trong các bài kiểm tra và đạt kết quả tốt trong môn Toán.
Các bài tập tương tự:
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về bài tập 5.39 và có thể tự giải các bài tập tương tự. Chúc các em học tập tốt!