Bài tập 7.21 trang 53 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 7.21 trang 53 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Thời gian chờ mua vé xem bóng đá của một số cổ động viên được cho như sau: a) Lập bảng tần số tương đối ghép nhóm. b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng cho bảng thống kê thu được ở câu a.
Đề bài
Thời gian chờ mua vé xem bóng đá của một số cổ động viên được cho như sau:

a) Lập bảng tần số tương đối ghép nhóm.
b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng cho bảng thống kê thu được ở câu a.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) + Tính tần số tương đối ứng với các giá trị trong mẫu dữ liệu: Nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\) có tần số \({m_i}\) thì có tần số tương đối là: \({f_i} = \frac{{{m_i}}}{n}.100\left( \% \right)\) với m là tổng tất cả các tần số có trong mẫu số liệu.
+ Lập bảng tần số tương đối ghép nhóm:

b) Cách vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng:
Bước 1: Chọn giá trị \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) đại diện cho các nhóm số liệu \(\left[ {{a_i};{a_{i + 1}}} \right)\) với \(i = 1,2,3,..,k\).
Bước 2: Vẽ trục ngang để biểu diễn các giá trị đại diện cho nhóm số liệu, vẽ trục đứng thể hiện tần số tương đối.
Bước 3: Với mỗi giá trị đại diện \({x_i}\) trên trục ngang và tần số tương đối \({f_i}\) tương ứng, ta xác định một điểm \({M_i}\left( {{x_i};{f_i}} \right)\). Nối các điểm liên tiếp với nhau.
Bước 4: Ghi chú giải cho các trục, các điểm và tiêu đề của biểu đồ.
Lời giải chi tiết
a) Tổng số cổ động viên mua vé là: \(15 + 38 + 50 + 27 + 20 + 10 = 160\)
Tần số tương đối tương ứng với các nhóm số liệu thời gian \(\left[ {0;5} \right)\); \(\left[ {5;10} \right)\); \(\left[ {10;15} \right)\); \(\left[ {15;20} \right)\); \(\left[ {20;25} \right)\); \(\left[ {25;30} \right)\) là:
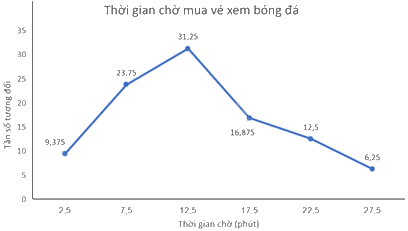
\(\frac{{15}}{{160}} = 9,375\% ;\frac{{38}}{{160}} = 23,75\% ;\frac{{50}}{{160}} = 31,25\% ;\frac{{27}}{{160}} = 16,875\% ;\frac{{20}}{{160}} = 12,5\% ;\frac{{10}}{{160}} = 6,25\% \)
Do đó, ta có bảng tần số tương đối ghép nhóm:

b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng:
Bước 1: Chọn giá trị đại diện cho các nhóm số liệu ta có bảng sau:

Bước 2: Vẽ các trục.
Bước 3:Xác định các điểm, nối các điểm liên tiếp với nhau.
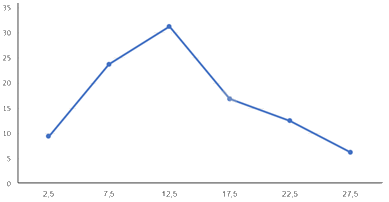
Bước 4: Ghi chú giải cho các trục, các điểm và tiêu đề của biểu đồ tần số tương đối ghép nhóm.
Bài tập 7.21 trang 53 SGK Toán 9 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc nhất và hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Trước khi đi vào giải bài tập, chúng ta cần phân tích kỹ đề bài để hiểu rõ yêu cầu và các dữ kiện đã cho. Bài toán thường mô tả một tình huống thực tế, ví dụ như tính chiều dài, chiều rộng của một hình chữ nhật, tính vận tốc, thời gian của một chuyển động, hoặc tính giá tiền của một sản phẩm. Dựa vào tình huống đó, chúng ta cần xác định các đại lượng liên quan và mối quan hệ giữa chúng.
(Nội dung lời giải chi tiết bài tập 7.21 sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, các phép tính chính xác và các giải thích rõ ràng. Lời giải sẽ được trình bày theo từng bước để học sinh dễ theo dõi và hiểu được.)
Ví dụ, nếu bài toán yêu cầu tính chiều dài và chiều rộng của một hình chữ nhật, ta có thể làm như sau:
Ngoài bài tập 7.21, còn rất nhiều bài tập tương tự trong chương trình Toán 9 Kết nối tri thức. Để giải các bài tập này, chúng ta có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và kỹ năng giải bài tập, các em học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng, giúp các em học sinh rèn luyện và nâng cao khả năng giải toán.
Bài tập 7.21 trang 53 SGK Toán 9 tập 2 là một bài tập quan trọng trong chương trình Toán 9 Kết nối tri thức. Việc nắm vững kiến thức và phương pháp giải bài tập này sẽ giúp các em học sinh tự tin giải các bài tập tương tự và đạt kết quả tốt trong các kỳ thi và kiểm tra. Hy vọng rằng, với lời giải chi tiết và hướng dẫn cụ thể của Giaitoan.edu.vn, các em học sinh sẽ hiểu rõ bản chất của bài toán và tự tin giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục tri thức. Chúc các em học tập tốt!