Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Chúng tôi giúp bạn nắm vững kiến thức và tự tin giải quyết các bài toán trong sách giáo khoa.
Ở bài viết này, chúng ta sẽ cùng nhau khám phá lời giải cho mục 1 trang 102 SGK Toán 9 tập 2 - Kết nối tri thức. Hãy cùng bắt đầu!
Tìm một vài hình ảnh của hình cầu, mặt cầu trong thực tế.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 103 SGK Toán 9 Kết nối tri thức
Khi cắt một hình cầu bởi một mặt phẳng đi qua tâm của hình cầu đó được một hình tròn có diện tích \(25\pi \;c{m^2}\). Tính bán kính của hình cầu.
Phương pháp giải:
+ Chỉ ra bán kính của hình tròn là bán kính của hình cầu.
+ Sử dụng công thức tính diện tích hình tròn: \(S = \pi {R^2}\) để tính R.
Lời giải chi tiết:
Do cắt hình cầu bởi một mặt phẳng đi qua tâm của hình cầu nên bán kính của hình tròn bằng bán kính của hình cầu.
Gọi R là bán kính của hình cầu.
Khi đó ta có: \(\pi {R^2} = 25\pi \), suy ra \({R^2} = 25\) nên \(R = 5cm\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 102 SGK Toán 9 Kết nối tri thức
Khi cắt đôi một quả cam có dạng hình cầu (H.10.22b), em thấy mặt cắt có dạng hình gì?

Phương pháp giải:
Quan sát thấy mặt cắt của quả cam có dạng hình tròn.
Lời giải chi tiết:
Mặt cắt của quả cam có dạng hình tròn.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 102 SGK Toán 9 Kết nối tri thức
Sọ dừa được xem là có dạng hình cầu. Người ta cắt sọ dừa khô để làm gáo dừa (H.10.22a). Em thấy miệng gáo có dạng hình gì?

Phương pháp giải:
Quan sát thấy miệng gáo có dạng hình tròn.
Lời giải chi tiết:
Miệng gáo có dạng hình tròn.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 102 SGK Toán 9 Kết nối tri thức
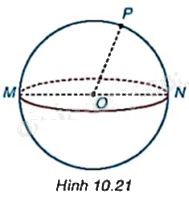
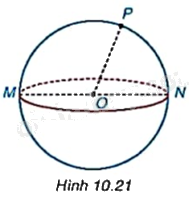
Kể tên các bán kính còn lại của mặt cầu trong Hình 10.21.
Phương pháp giải:
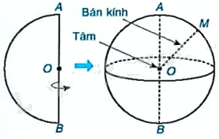
Mặt cầu và hình cầu có dạng:
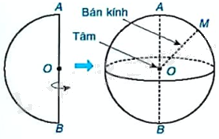
Lời giải chi tiết:
Bán kính còn lại của mặt cầu là OM, ON.
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 102 SGK Toán 9 Kết nối tri thức
Tìm một vài hình ảnh của hình cầu, mặt cầu trong thực tế.
Phương pháp giải:
Mặt cầu và hình cầu có dạng:
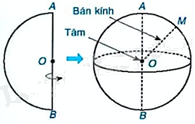
Lời giải chi tiết:
Một vài hình ảnh của hình cầu, mặt cầu trong thực tế:

Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 102 SGK Toán 9 Kết nối tri thức
Tìm một vài hình ảnh của hình cầu, mặt cầu trong thực tế.
Phương pháp giải:
Mặt cầu và hình cầu có dạng:
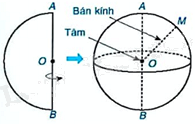
Lời giải chi tiết:
Một vài hình ảnh của hình cầu, mặt cầu trong thực tế:

Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 102 SGK Toán 9 Kết nối tri thức
Kể tên các bán kính còn lại của mặt cầu trong Hình 10.21.
Phương pháp giải:
Mặt cầu và hình cầu có dạng:
Lời giải chi tiết:
Bán kính còn lại của mặt cầu là OM, ON.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 102 SGK Toán 9 Kết nối tri thức
Sọ dừa được xem là có dạng hình cầu. Người ta cắt sọ dừa khô để làm gáo dừa (H.10.22a). Em thấy miệng gáo có dạng hình gì?

Phương pháp giải:
Quan sát thấy miệng gáo có dạng hình tròn.
Lời giải chi tiết:
Miệng gáo có dạng hình tròn.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 102 SGK Toán 9 Kết nối tri thức
Khi cắt đôi một quả cam có dạng hình cầu (H.10.22b), em thấy mặt cắt có dạng hình gì?

Phương pháp giải:
Quan sát thấy mặt cắt của quả cam có dạng hình tròn.
Lời giải chi tiết:
Mặt cắt của quả cam có dạng hình tròn.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 103 SGK Toán 9 Kết nối tri thức
Khi cắt một hình cầu bởi một mặt phẳng đi qua tâm của hình cầu đó được một hình tròn có diện tích \(25\pi \;c{m^2}\). Tính bán kính của hình cầu.
Phương pháp giải:
+ Chỉ ra bán kính của hình tròn là bán kính của hình cầu.
+ Sử dụng công thức tính diện tích hình tròn: \(S = \pi {R^2}\) để tính R.
Lời giải chi tiết:
Do cắt hình cầu bởi một mặt phẳng đi qua tâm của hình cầu nên bán kính của hình tròn bằng bán kính của hình cầu.
Gọi R là bán kính của hình cầu.
Khi đó ta có: \(\pi {R^2} = 25\pi \), suy ra \({R^2} = 25\) nên \(R = 5cm\).
Mục 1 trang 102 SGK Toán 9 tập 2 - Kết nối tri thức thường xoay quanh các chủ đề về hàm số bậc hai, bao gồm định nghĩa, tính chất, đồ thị và ứng dụng. Việc nắm vững kiến thức nền tảng về hàm số là vô cùng quan trọng để giải quyết các bài toán liên quan.
Hàm số bậc hai có dạng tổng quát là y = ax2 + bx + c, trong đó a, b, c là các hệ số và a ≠ 0. Các yếu tố quan trọng cần xác định là:
Để giải các bài tập trong mục 1 trang 102 SGK Toán 9 tập 2 - Kết nối tri thức, bạn có thể áp dụng các phương pháp sau:
Bài tập: Tìm tọa độ đỉnh của parabol y = 2x2 - 8x + 6.
Lời giải:
Hệ số a = 2, b = -8, c = 6.
Tọa độ đỉnh của parabol là:
x0 = -b/2a = -(-8)/(2*2) = 2
y0 = 2*(2)2 - 8*2 + 6 = 8 - 16 + 6 = -2
Vậy, tọa độ đỉnh của parabol là I(2; -2).
Để nắm vững kiến thức về hàm số bậc hai, bạn nên luyện tập thường xuyên với các bài tập khác nhau. Hãy tìm kiếm thêm các tài liệu tham khảo, bài giảng online hoặc tham gia các khóa học toán để nâng cao kỹ năng giải toán của mình.
Hàm số bậc hai có nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng rằng, với những kiến thức và phương pháp giải bài tập được trình bày trong bài viết này, bạn sẽ tự tin hơn khi đối mặt với các bài toán về hàm số bậc hai trong SGK Toán 9 tập 2 - Kết nối tri thức. Chúc bạn học tập tốt!