Chào mừng bạn đến với bài học về Lý thuyết Bảng tần số tương đối và Biểu đồ tần số tương đối trong chương trình Toán 9 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về chủ đề này.
Chúng ta sẽ cùng nhau tìm hiểu cách xây dựng bảng tần số tương đối, cách vẽ biểu đồ tần số tương đối và ứng dụng của chúng trong việc phân tích dữ liệu thống kê.
1. Bảng tần số tương đối Cho dãy dữ liệu \({x_1},{x_2},...,{x_n}\). Tần số tương đối \({t_i}\) của giá trị \({x_i}\) là tỉ số giữa tần số của \({x_i}\) (gọi là \({m_i}\)) với n.
1. Bảng tần số tương đối
Cho dãy dữ liệu \({x_1},{x_2},...,{x_n}\). Tần số tương đối \({t_i}\) của giá trị \({x_i}\) là tỉ số giữa tần số của \({x_i}\) (gọi là \({m_i}\)) với n. Bảng sau đây được gọi là bảng tần số tương đối.
trong đó \(n = {m_1} + ... + {m_k}\) và \({f_1} = \frac{{{m_1}}}{n}.100\left( \% \right)\) là tần số tương đối của \({x_1},...\), \({f_k} = \frac{{{m_k}}}{n}.100\left( \% \right)\) là tần số tương đối của \({x_k}\). Bảng tần số tương đối còn được cho dưới dạng cột:
|
Ví dụ: Cho bảng thống kê số anh, chị, em ruột của các bạn trong lớp:

Tổng số bạn là \(n = 30\).
Số anh, chị, em ruột là \({x_1} = 0;{x_2} = 1;{x_3} = 2;{x_4} = 3\) tương ứng với \({m_1} = 8;{m_2} = 12;{m_3} = 6,{m_4} = 4\).
Do đó các tần số tương đối cho các giá trị \({x_1},{x_2},{x_3},{x_4}\) lần lượt là:
\({f_1} = \frac{8}{{30}} \approx 26,7\% ;{f_2} = \frac{{12}}{{30}} = 40\% ;\)
\({f_3} = \frac{6}{{30}} = 20\% ;{f_4} = \frac{4}{{30}} \approx 13,3\% .\)
Ta có bảng tần số tương đối sau:

Nhận xét: Tần số tương đối của một giá trị là ước lượng cho xác suất xuất hiện giá trị đó.
2. Biểu đồ tần số tương đối
- Biểu đồ biểu diễn bảng tần số tương đối được gọi là biểu đồ tần số tương đối. Dạng thường gặp của biểu đồ tần số tương đối là biểu đồ cột và biểu đồ hình quạt tròn. - Để vẽ biểu đồ hình quạt tròn ta thực hiện các bước sau: Bước 1. Xác định số đo cung tương ứng của các hình quạt dùng để biểu diễn tần số tương đối của các giá trị theo công thức \(360^\circ .{f_i}\) với \(i = 1,...,k\). Bước 2. Vẽ hình tròn và chia hình tròn thành các hình quạt có số đo cung tương ứng được xác định trong Bước 1. Bước 3. Định dạng các hình quạt tròn (thường bằng cách tô màu), ghi tần số tương đối, chú giải và tiêu đề. |
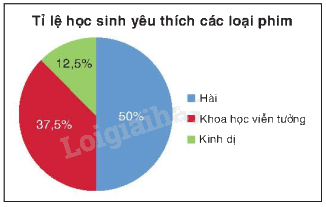
Ví dụ: Vẽ biểu đồ hình quạt tròn biểu diễn bảng tần số tương đối về loại phim yêu thích của các học sinh trong lớp 9A như sau:

Bước 1. Xác định số đo cung tương ứng của các hình quạt biểu diễn các tần số tương đối cho mỗi loại phim:
Hài: \(360^\circ .50\% = 180^\circ \);
Khoa học viễn tưởng: \(360^\circ .37,5\% = 135^\circ \);
Kinh dị: \(360^\circ .12,5\% = 45^\circ \).
Bước 2. Vẽ hình tròn và chia hình tròn thành các hình quạt.
Bước 3. Định dạng các hình quạt tròn, ghi tỉ lệ phần trăm, chú giải và tiêu đề.
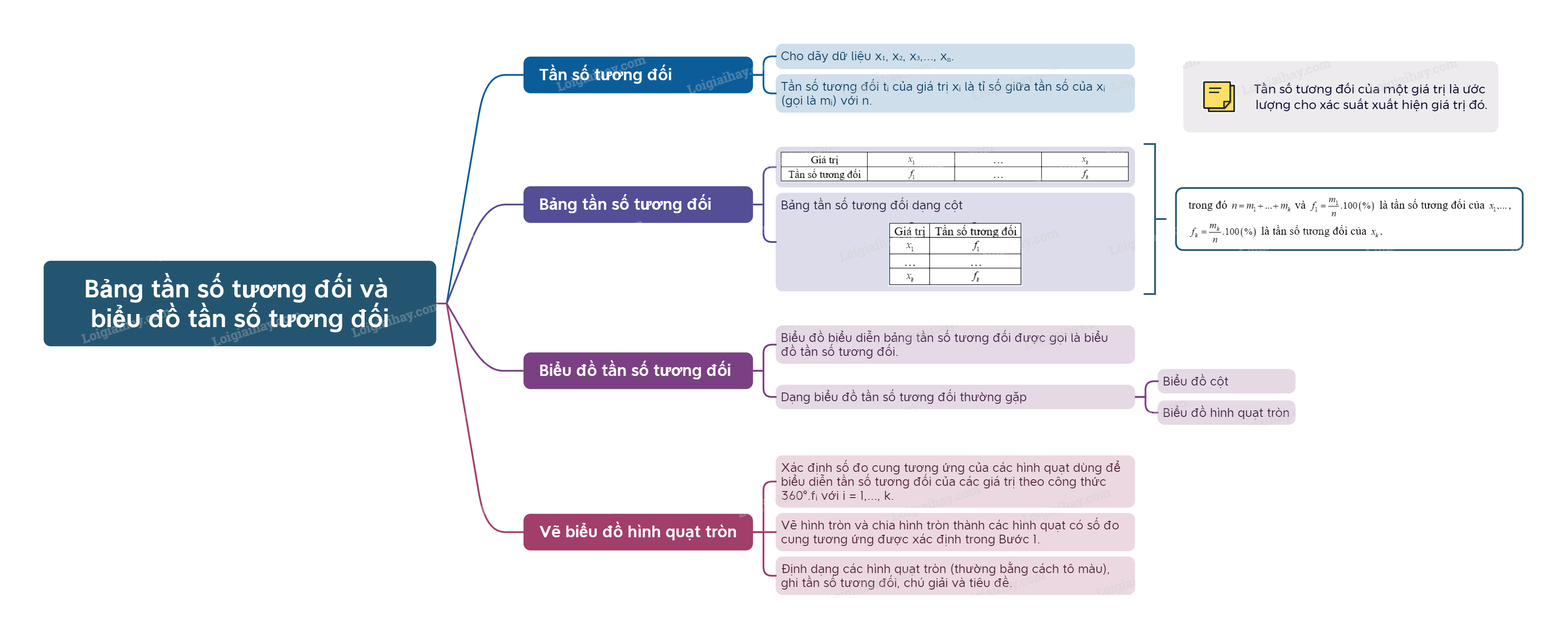
Trong chương trình Toán 9 Kết nối tri thức, chủ đề về thống kê và xác suất đóng vai trò quan trọng trong việc giúp học sinh rèn luyện tư duy logic và khả năng phân tích dữ liệu. Một trong những nội dung cốt lõi của chủ đề này là lý thuyết về bảng tần số tương đối và biểu đồ tần số tương đối. Bài viết này sẽ cung cấp một cái nhìn chi tiết và dễ hiểu về các khái niệm này, cùng với các ví dụ minh họa cụ thể.
Trước khi đi sâu vào bảng tần số tương đối và biểu đồ tần số tương đối, chúng ta cần nắm vững các khái niệm cơ bản về tần số.
Tần số tương đối thường được biểu diễn dưới dạng phần trăm (%) để dễ dàng so sánh và phân tích.
Bảng tần số tương đối là một bảng thống kê được sử dụng để trình bày tần số và tần số tương đối của các giá trị trong một tập dữ liệu. Bảng này giúp chúng ta dễ dàng nhận biết được sự phân bố của dữ liệu và các giá trị nào xuất hiện thường xuyên nhất.
Cấu trúc của bảng tần số tương đối:
| Giá trị (x) | Tần số (f) | Tần số tương đối (ftđ) | Tần số tương đối (%) |
|---|---|---|---|
| x1 | f1 | f1/N | (f1/N) * 100% |
| x2 | f2 | f2/N | (f2/N) * 100% |
| ... | ... | ... | ... |
Biểu đồ tần số tương đối là một biểu diễn trực quan của bảng tần số tương đối. Nó giúp chúng ta dễ dàng so sánh tần số tương đối của các giá trị khác nhau và nhận biết được xu hướng phân bố của dữ liệu.
Có nhiều loại biểu đồ tần số tương đối khác nhau, phổ biến nhất là:
Giả sử chúng ta có một tập dữ liệu về điểm kiểm tra Toán của 20 học sinh:
5, 6, 7, 8, 5, 6, 7, 9, 6, 7, 8, 8, 7, 6, 5, 7, 8, 9, 6, 7
Bước 1: Lập bảng tần số
| Điểm (x) | Tần số (f) |
|---|---|
| 5 | 3 |
| 6 | 4 |
| 7 | 5 |
| 8 | 4 |
| 9 | 2 |
Bước 2: Lập bảng tần số tương đối
| Điểm (x) | Tần số (f) | Tần số tương đối (ftđ) | Tần số tương đối (%) |
|---|---|---|---|
| 5 | 3 | 3/20 | 15% |
| 6 | 4 | 4/20 | 20% |
| 7 | 5 | 5/20 | 25% |
| 8 | 4 | 4/20 | 20% |
| 9 | 2 | 2/20 | 10% |
Bước 3: Vẽ biểu đồ tần số tương đối (ví dụ: biểu đồ cột)
Dựa vào bảng tần số tương đối, chúng ta có thể vẽ biểu đồ cột với trục hoành là điểm số và trục tung là tần số tương đối (%).
Bảng tần số tương đối và biểu đồ tần số tương đối có nhiều ứng dụng trong thực tế, bao gồm:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết Bảng tần số tương đối và Biểu đồ tần số tương đối Toán 9 Kết nối tri thức. Chúc bạn học tập tốt!