Bài tập 5.36 trang 112 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Đây là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 5.36, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho đường tròn (O) đường kính BC và điểm A (khác B và C). a) Chứng minh rằng nếu A nằm trên (O) thì ABC là một tam giác vuông; ngược lại, nếu ABC là tam giác vuông tại A thì nằm trên (O). b) Giả sử A là một trong hai giao điểm của đường tròn (B; BO) với đường tròn (O). Tính các góc của tam giác ABC. c) Với cùng giả thiết câu b), tính độ dài cung AC và diện tích hình quạt nằm trong (O) giới hạn bởi các bán kính OA và OC, biết rằng BC = 6 cm.
Đề bài
Cho đường tròn (O) đường kính BC và điểm A (khác B và C).
a) Chứng minh rằng nếu A nằm trên (O) thì ABC là một tam giác vuông; ngược lại, nếu ABC là tam giác vuông tại A thì nằm trên (O).
b) Giả sử A là một trong hai giao điểm của đường tròn (B; BO) với đường tròn (O). Tính các góc của tam giác ABC.
c) Với cùng giả thiết câu b), tính độ dài cung AC và diện tích hình quạt nằm trong (O) giới hạn bởi các bán kính OA và OC, biết rằng BC = 6 cm.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Tam giác có đường trung tuyến ứng với một cạnh và bằng nửa cạnh đấy là tam giác vuông
Diện tích hình quạt tròn bán kính R ứng với cung n0 là \(\frac{{\pi {R^2}.n}}{{360}}\)
Độ dài cung tròn n0 của đường tròn bán kính R là \(\frac{{\pi Rn}}{{180}}\)
Lời giải chi tiết
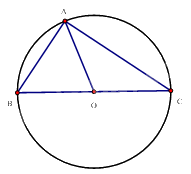
a) A nằm trên đường tròn tâm O nên AO = BO = CO
Tam giác ABC có AO là đường trung tuyến ứng với cạnh BC và \(AO = \frac{1}{2}BC\)
Nên tam giác ABC vuông tại A.
Chiều ngược lại:
Nếu tam giác ABC vuông tại A, gọi O là trung điểm của cạnh huyền BC thì ta có AO = BO = CO (tính chất đường trung tuyến trong tam giác vuông)
Từ đó ta có A, B, C thuộc đường tròn tâm O.
b)
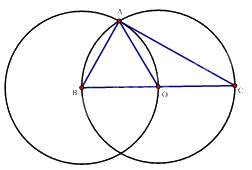
A là giao điểm của hai đường tròn (O) và (B) nên A thuộc (O) đường kính BC nên tam giác BAC vuông tại A.
Tam giác ABO có \(AB = BO = AO\) nên tam giác ABO đều suy ra \(\widehat {ABO} = \widehat {AOB} = \widehat {BAO} = {60^0}\)
Tam giác ABC vuông tại A nên \(\widehat B + \widehat C = {90^0}\) hay \({60^0} + \widehat C = {90^0}\) hay \(\widehat C = {30^0}\)
c) Ta có: \(\widehat {AOB} + \widehat {AOC} = {180^0}\) (hai góc kề bù)
nên \({60^0} + \widehat {AOC} = {180^0}\) hay \(\widehat {AOC} = {180^0} - {60^0} = {120^0}\)
Đường kính BC = 6 cm nên bán kỉnh đường tròn (O) là \(6:2 = 3\) cm
Độ dài cung AC là \(\frac{{2\pi .3.120}}{{360}} = 2\pi \) cm
Diện tích phần quạt chứa OA, OC là \(\frac{{\pi {R^2}.120}}{{360}} = \frac{{{3^2}\pi .120}}{{360}} = 3\pi \left( {c{m^2}} \right)\)
Bài tập 5.36 yêu cầu chúng ta xét hàm số bậc nhất y = (m-1)x + 3. Để hàm số này là hàm số bậc nhất, hệ số a (tức là m-1) phải khác 0. Điều này có nghĩa là m ≠ 1.
Đề bài yêu cầu tìm điều kiện của m để hàm số y = (m-1)x + 3 là hàm số bậc nhất. Để giải bài toán này, chúng ta cần nắm vững định nghĩa của hàm số bậc nhất và điều kiện để một hàm số là hàm số bậc nhất.
Để hàm số y = (m-1)x + 3 là hàm số bậc nhất, ta cần có:
m - 1 ≠ 0
Suy ra:
m ≠ 1
Vậy, điều kiện của m để hàm số y = (m-1)x + 3 là hàm số bậc nhất là m ≠ 1.
Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, và a ≠ 0. Hàm số bậc nhất có đồ thị là một đường thẳng. Hệ số a được gọi là hệ số góc của đường thẳng, và nó xác định độ dốc của đường thẳng. Hệ số b được gọi là tung độ gốc, và nó là tung độ của điểm mà đường thẳng cắt trục Oy.
Ví dụ 1: Tìm m để hàm số y = (2m-1)x + 5 là hàm số bậc nhất.
Giải: Để hàm số là hàm số bậc nhất, ta cần có 2m - 1 ≠ 0. Suy ra m ≠ 1/2.
Ví dụ 2: Hàm số y = -3x + 2 có hệ số góc và tung độ gốc là bao nhiêu?
Giải: Hệ số góc là a = -3, tung độ gốc là b = 2.
Để nắm vững kiến thức về hàm số bậc nhất, các em học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác.
Bài tập 5.36 trang 112 SGK Toán 9 tập 1 là một bài tập cơ bản về hàm số bậc nhất. Việc nắm vững kiến thức về hàm số bậc nhất sẽ giúp các em học sinh giải quyết các bài toán phức tạp hơn trong chương trình Toán 9.
| Khái niệm | Định nghĩa |
|---|---|
| Hàm số bậc nhất | Hàm số có dạng y = ax + b, trong đó a và b là các số thực, và a ≠ 0. |
| Hệ số góc | Hệ số a trong hàm số y = ax + b. |
| Tung độ gốc | Hệ số b trong hàm số y = ax + b. |
SGK Toán 9 tập 1 - Kết nối tri thức
Sách bài tập Toán 9
Các trang web học toán online uy tín