Bài tập 5.5 trang 90 SGK Toán 9 tập 1 thuộc chương trình Kết nối tri thức là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng giải phương trình bậc hai. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về công thức nghiệm, định lý Vi-et và các phương pháp giải phương trình khác nhau.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 5.5 trang 90 SGK Toán 9 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho nửa đường tròn đường kính AB và một điểm M tùy ý thuộc nửa đường tròn đó. Chứng minh rằng khoảng cách từ M đến AB không lớn hơn (frac{{AB}}{2}.)
Đề bài
Cho nửa đường tròn đường kính AB và một điểm M tùy ý thuộc nửa đường tròn đó. Chứng minh rằng khoảng cách từ M đến AB không lớn hơn \(\frac{{AB}}{2}.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Gọi H là hình chiếu của M trên AB.
Khi đó khoảng cách từ M đến AB bằng độ dài đoạn MH.
Xét tam giác MHO vuông tại H có: \(MH \le MO = \frac{{AB
Lời giải chi tiết
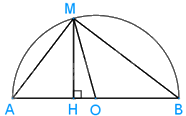
Gọi H là hình chiếu của M trên AB.
Khi đó khoảng cách từ M đến AB bằng độ dài đoạn MH.
Xét tam giác MHO vuông tại H có: \(MH \le MO\)
Lại có: \(MO = \frac{{AB}}{2}\)(do AB là đường kính, OM là bán kính của đường tròn (O)).
Vậy \(MH \le \frac{{AB}}{2}.\)
Bài tập 5.5 trang 90 SGK Toán 9 tập 1 - Kết nối tri thức yêu cầu giải phương trình bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Để giải bài tập 5.5, chúng ta cần xác định các hệ số a, b, c của phương trình. Sau đó, tính Δ và sử dụng công thức nghiệm để tìm ra các nghiệm của phương trình. Cuối cùng, kiểm tra lại kết quả bằng cách thay các nghiệm vào phương trình ban đầu.
Ví dụ, xét phương trình 2x2 - 5x + 2 = 0. Ta có a = 2, b = -5, c = 2. Tính Δ = (-5)2 - 4 * 2 * 2 = 25 - 16 = 9. Vì Δ > 0, phương trình có hai nghiệm phân biệt:
x1 = (5 + √9) / (2 * 2) = (5 + 3) / 4 = 2
x2 = (5 - √9) / (2 * 2) = (5 - 3) / 4 = 0.5
Kiểm tra lại:
Với x = 2: 2 * 22 - 5 * 2 + 2 = 8 - 10 + 2 = 0
Với x = 0.5: 2 * (0.5)2 - 5 * 0.5 + 2 = 0.5 - 2.5 + 2 = 0
Ngoài bài tập 5.5, còn rất nhiều bài tập tương tự yêu cầu giải phương trình bậc hai. Để giải các bài tập này, bạn có thể áp dụng các phương pháp sau:
Để nắm vững kiến thức về phương trình bậc hai, bạn nên luyện tập thêm các bài tập khác. Bạn có thể tìm thấy các bài tập này trong SGK Toán 9 tập 1, các sách bài tập Toán 9 hoặc trên các trang web học Toán online.
Bài tập 5.5 trang 90 SGK Toán 9 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải phương trình bậc hai. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài tập và nắm vững kiến thức Toán 9.