Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 1 trang 60, 61 sách giáo khoa Toán 9 tập 1 chương trình Kết nối tri thức.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bài giải này với mục tiêu giúp các em nắm vững kiến thức và tự tin giải quyết các bài tập tương tự.
Kí hiệu V là thể tích của hình lập phương với cạnh x. Hãy thay dấu “?” trong bảng sau bằng các giá trị thích hợp.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 61 SGK Toán 9 Kết nối tri thức
Tính:
a) \(\sqrt[3]{{125}};\)
b) \(\sqrt[3]{{0,008}};\)
c) \(\sqrt[3]{{\frac{{ - 8}}{{27}}}}.\)
Phương pháp giải:
Căn bậc ba của một số a là x sao cho \({x^3} = a\). Kí hiệu \(\sqrt[3]{a} = x\)
Lời giải chi tiết:
a) \(\sqrt[3]{{125}} = 5\)
b) \(\sqrt[3]{{0,008}} = 0,2\)
c) \(\sqrt[3]{{\frac{{ - 8}}{{27}}}} = \frac{{ - 2}}{3}\)
Video hướng dẫn giải
Trả lời câu hỏi Thử thách nhỏ trang 61 SGK Toán 9 Kết nối tri thức
Có thể xếp 125 khối lập phương đơn vị (có cạnh bằng 1 cm) thành một khối lập phương lớn không?
Phương pháp giải:
Giả sử có thể xếp được khối lập phương mới có cạnh là x, thì thể tích của hình lập phương mới bằng thể tích của 125 hình lập phương.
Lời giải chi tiết:
Thể tích của khối lập phương đơn vị là \({1^3} = 1\left( {c{m^3}} \right)\)
Do đó thể tích của 125 khối lập phương là \(125.1 = 125\left( {c{m^3}} \right)\)
Giả sử xếp được 125 khối lập phương thành khối lập phương lớn cạnh là x cm, thì ta có thể tích của hình lập phương mới là \({x^3}\left( {c{m^3}} \right)\)
Từ đó ta có \({x^3} = 125\) hay \(x = 5\)
Vậy ta có thể xếp được 125 khối lập phương đơn vị thành một khối lập phương mới cạnh là 5 cm.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 60 SGK Toán 9 Kết nối tri thức
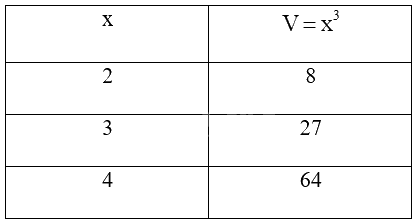
Kí hiệu V là thể tích của hình lập phương với cạnh x. Hãy thay dấu “?” trong bảng sau bằng các giá trị thích hợp.

Phương pháp giải:
Thay V vào công thức \(V=x^3\) để tìm x điền vào ?
Lời giải chi tiết:
Ta có \({3^3} = 27;{4^3} = 64\), ta được bảng sau:
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 61 SGK Toán 9 Kết nối tri thức
Sử dụng MTCT, tính \(\sqrt[3]{{45}}\) và làm tròn kết quả với độ chính xác 0,005.
Phương pháp giải:
Bấm MTCT ta được kết quả \(\sqrt[3]{{45}} = 3,556893304\) và làm tròn với độ chính xác 0,005 chính là lấy 2 chữ số ở phần thập phân.
Lời giải chi tiết:
Bấm MTCT ta được:
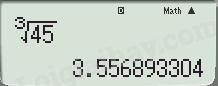
Làm tròn với độ chính xác 0,005 ta được: \(\sqrt[3]{{45}} \approx 3,56\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 60 SGK Toán 9 Kết nối tri thức
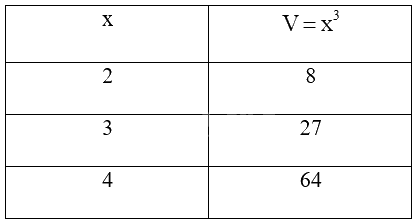
Kí hiệu V là thể tích của hình lập phương với cạnh x. Hãy thay dấu “?” trong bảng sau bằng các giá trị thích hợp.

Phương pháp giải:
Thay V vào công thức \(V=x^3\) để tìm x điền vào ?
Lời giải chi tiết:
Ta có \({3^3} = 27;{4^3} = 64\), ta được bảng sau:
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 61 SGK Toán 9 Kết nối tri thức
Tính:
a) \(\sqrt[3]{{125}};\)
b) \(\sqrt[3]{{0,008}};\)
c) \(\sqrt[3]{{\frac{{ - 8}}{{27}}}}.\)
Phương pháp giải:
Căn bậc ba của một số a là x sao cho \({x^3} = a\). Kí hiệu \(\sqrt[3]{a} = x\)
Lời giải chi tiết:
a) \(\sqrt[3]{{125}} = 5\)
b) \(\sqrt[3]{{0,008}} = 0,2\)
c) \(\sqrt[3]{{\frac{{ - 8}}{{27}}}} = \frac{{ - 2}}{3}\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 61 SGK Toán 9 Kết nối tri thức
Sử dụng MTCT, tính \(\sqrt[3]{{45}}\) và làm tròn kết quả với độ chính xác 0,005.
Phương pháp giải:
Bấm MTCT ta được kết quả \(\sqrt[3]{{45}} = 3,556893304\) và làm tròn với độ chính xác 0,005 chính là lấy 2 chữ số ở phần thập phân.
Lời giải chi tiết:
Bấm MTCT ta được:
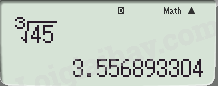
Làm tròn với độ chính xác 0,005 ta được: \(\sqrt[3]{{45}} \approx 3,56\)
Video hướng dẫn giải
Trả lời câu hỏi Thử thách nhỏ trang 61 SGK Toán 9 Kết nối tri thức
Có thể xếp 125 khối lập phương đơn vị (có cạnh bằng 1 cm) thành một khối lập phương lớn không?
Phương pháp giải:
Giả sử có thể xếp được khối lập phương mới có cạnh là x, thì thể tích của hình lập phương mới bằng thể tích của 125 hình lập phương.
Lời giải chi tiết:
Thể tích của khối lập phương đơn vị là \({1^3} = 1\left( {c{m^3}} \right)\)
Do đó thể tích của 125 khối lập phương là \(125.1 = 125\left( {c{m^3}} \right)\)
Giả sử xếp được 125 khối lập phương thành khối lập phương lớn cạnh là x cm, thì ta có thể tích của hình lập phương mới là \({x^3}\left( {c{m^3}} \right)\)
Từ đó ta có \({x^3} = 125\) hay \(x = 5\)
Vậy ta có thể xếp được 125 khối lập phương đơn vị thành một khối lập phương mới cạnh là 5 cm.
Mục 1 trang 60, 61 SGK Toán 9 tập 1 - Kết nối tri thức thường xoay quanh các chủ đề về hàm số bậc nhất, bao gồm định nghĩa, tính chất, đồ thị và ứng dụng của hàm số. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững các khái niệm cơ bản và các phương pháp giải toán liên quan.
Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0. 'a' được gọi là hệ số góc, quyết định độ dốc của đường thẳng biểu diễn hàm số. 'b' là tung độ gốc, là giao điểm của đường thẳng với trục Oy.
Đồ thị của hàm số y = ax + b là một đường thẳng. Để vẽ đồ thị, ta cần xác định hai điểm thuộc đường thẳng, ví dụ như giao điểm với trục Ox và trục Oy.
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ như:
Bài 1: (Ví dụ) Cho hàm số y = 2x - 1. Hãy xác định hệ số góc và tung độ gốc của hàm số. Vẽ đồ thị của hàm số.Giải: Hệ số góc a = 2, tung độ gốc b = -1. Để vẽ đồ thị, ta xác định hai điểm: A(0, -1) và B(1, 1). Nối A và B, ta được đồ thị của hàm số.
Bài 2: (Ví dụ) Một người đi xe đạp với vận tốc 15km/h. Hãy viết công thức tính quãng đường đi được s theo thời gian t.Giải: s = 15t
Để giải các bài tập về hàm số bậc nhất một cách nhanh chóng và chính xác, các em cần:
Các bài tập về hàm số bậc nhất thường gặp các dạng sau:
Ngoài SGK Toán 9 tập 1 - Kết nối tri thức, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 1 trang 60, 61 SGK Toán 9 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!