Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách giáo khoa Toán 9 Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Người ta thấy rằng lượng sơn cần dùng để sơn kín một mặt cầu bán kính R bằng với lượng sơn cần dùng để sơn kín một hình tròn bán kính 2R (khi độ dày của lớp sơn như nhau) (H.10.24). Từ đó, em hãy dự đoán công thức tính diện tích mặt cầu bán kính R.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 103SGK Toán 9 Kết nối tri thức
Sử dụng một hình cầu bán kính R và một cốc thủy tinh có dạng hình trụ bán kính đáy R, chiều cao 2R. Ban đầu để hình cầu nằm khít trong chiếc cốc đầy nước. Ta nhấc hình cầu ra khỏi cốc thủy tinh hình trụ (H.10.25).
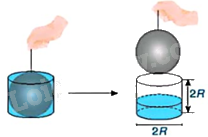
Đo độ cao cột nước còn lại trong chiếc cốc, ta thấy độ cao này chỉ bằng \(\frac{1}{3}\) chiều cao của chiếc cốc hình trụ. Từ đó, em hãy dự đoán công thức tính thể tích hình cầu bán kính R.
Phương pháp giải:
+ Thể tích của nước trong cốc khi hình cầu trong cốc: \({V_1}\).
+ Thể tích của nước trong cốc khi bỏ hình cầu ra ngoài: \({V_2}\).
+ Thể tích của hình cầu là: \(V = {V_1} - {V_2}\) .
+ Dự đoán công thức tính thể tích hình cầu.
Lời giải chi tiết:
Thể tích của nước trong cốc khi hình cầu trong cốc:
\({V_1} = \pi {R^2}.2R = 2\pi {R^3}\).
Thể tích của nước trong cốc khi bỏ hình cầu ra ngoài:
\({V_2} = \pi {R^2}.\frac{1}{3}.2R = \frac{2}{3}\pi {R^3}\).
Thể tích của hình cầu là:
\(V = {V_1} - {V_2} = 2\pi {R^3} - \frac{2}{3}\pi {R^3} = \frac{4}{3}\pi {R^3}\).
Dự đoán công thức tính thể tích hình cầu bán kính R:
\(V = \frac{4}{3}\pi {R^3}\).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 104SGK Toán 9 Kết nối tri thức
Em hãy trả lời câu hỏi của tình huống mở đầu.
Quả bóng đá theo tiêu chuẩn FIFA (liên đoàn bóng đá thế giới) có dạng hình cầu với đường kính khoảng 22cm (H.10.18). Khi bơm căng quả bóng thì thể tích quả bóng bằng bao nhiêu?

Phương pháp giải:
Thể tích hình cầu bán kính R là: \(V = \frac{4}{3}\pi {R^3}\).
Lời giải chi tiết:
Bán kính quả bóng là:
\(R = 22:2 = 11\left( {cm} \right)\)
Thể tích quả bóng là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.11^3} = \frac{{5324}}{3}\pi \left( {c{m^3}} \right)\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 103 SGK Toán 9 Kết nối tri thức
Người ta thấy rằng lượng sơn cần dùng để sơn kín một mặt cầu bán kính R bằng với lượng sơn cần dùng để sơn kín một hình tròn bán kính 2R (khi độ dày của lớp sơn như nhau) (H.10.24). Từ đó, em hãy dự đoán công thức tính diện tích mặt cầu bán kính R.
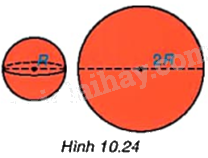
Phương pháp giải:
Diện tích hình tròn bán kính 2R là: \(S = \pi {\left( {2R} \right)^2}\), từ đó suy ra công thức tính diện tích mặt cầu.
Lời giải chi tiết:
Diện tích hình tròn bán kính 2R là: \(S = \pi {\left( {2R} \right)^2} = 4\pi {R^2}\).
Vì lượng sơn cần dùng để sơn kín một mặt cầu bán kính R bằng với lượng sơn cần dùng để sơn kín một hình tròn bán kính 2R nên dự đoán công thức tính diện tích mặt cầu là bán kính R là: \(S = 4\pi {R^2}\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 105 SGK Toán 9 Kết nối tri thức
Khinh khí cầu đầu tiên được phát minh bởi anh em nhà Montgolfler (người Pháp) vào năm 1782. Chuyến bay đầu tiên của hai anh em trên khinh khí cầu được thực hiện vào ngày 4 tháng 6 năm 1783 trên bầu trời Place des Cordeliers ở Annonay (nước Pháp) (theo cand.com.vn). Giả sử một khinh khí cầu có dạng hình cầu với đường kính bằng 11m. Tính diện tích mặt khinh khí cầu đó (làm tròn kết quả đến hàng đơn vị của \({m^2}\)).

Phương pháp giải:
+ Tính bán kính khinh khí cầu R.
+ Diện tích mặt khinh khí cầu bán kính R là: \(S = 4\pi {R^2}\).
Lời giải chi tiết:
Bán kính khinh khí cầu là: \(R = \frac{{11}}{2}m\).
Diện tích mặt khinh khí cầu là:
\(S = 4\pi {R^2} = 4\pi .{\left( {\frac{{11}}{2}} \right)^2} = 121\pi \approx 380\left( {{m^2}} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 103 SGK Toán 9 Kết nối tri thức
Người ta thấy rằng lượng sơn cần dùng để sơn kín một mặt cầu bán kính R bằng với lượng sơn cần dùng để sơn kín một hình tròn bán kính 2R (khi độ dày của lớp sơn như nhau) (H.10.24). Từ đó, em hãy dự đoán công thức tính diện tích mặt cầu bán kính R.
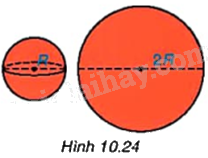
Phương pháp giải:
Diện tích hình tròn bán kính 2R là: \(S = \pi {\left( {2R} \right)^2}\), từ đó suy ra công thức tính diện tích mặt cầu.
Lời giải chi tiết:
Diện tích hình tròn bán kính 2R là: \(S = \pi {\left( {2R} \right)^2} = 4\pi {R^2}\).
Vì lượng sơn cần dùng để sơn kín một mặt cầu bán kính R bằng với lượng sơn cần dùng để sơn kín một hình tròn bán kính 2R nên dự đoán công thức tính diện tích mặt cầu là bán kính R là: \(S = 4\pi {R^2}\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 103SGK Toán 9 Kết nối tri thức
Sử dụng một hình cầu bán kính R và một cốc thủy tinh có dạng hình trụ bán kính đáy R, chiều cao 2R. Ban đầu để hình cầu nằm khít trong chiếc cốc đầy nước. Ta nhấc hình cầu ra khỏi cốc thủy tinh hình trụ (H.10.25).
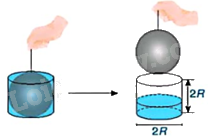
Đo độ cao cột nước còn lại trong chiếc cốc, ta thấy độ cao này chỉ bằng \(\frac{1}{3}\) chiều cao của chiếc cốc hình trụ. Từ đó, em hãy dự đoán công thức tính thể tích hình cầu bán kính R.
Phương pháp giải:
+ Thể tích của nước trong cốc khi hình cầu trong cốc: \({V_1}\).
+ Thể tích của nước trong cốc khi bỏ hình cầu ra ngoài: \({V_2}\).
+ Thể tích của hình cầu là: \(V = {V_1} - {V_2}\) .
+ Dự đoán công thức tính thể tích hình cầu.
Lời giải chi tiết:
Thể tích của nước trong cốc khi hình cầu trong cốc:
\({V_1} = \pi {R^2}.2R = 2\pi {R^3}\).
Thể tích của nước trong cốc khi bỏ hình cầu ra ngoài:
\({V_2} = \pi {R^2}.\frac{1}{3}.2R = \frac{2}{3}\pi {R^3}\).
Thể tích của hình cầu là:
\(V = {V_1} - {V_2} = 2\pi {R^3} - \frac{2}{3}\pi {R^3} = \frac{4}{3}\pi {R^3}\).
Dự đoán công thức tính thể tích hình cầu bán kính R:
\(V = \frac{4}{3}\pi {R^3}\).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 104SGK Toán 9 Kết nối tri thức
Em hãy trả lời câu hỏi của tình huống mở đầu.
Quả bóng đá theo tiêu chuẩn FIFA (liên đoàn bóng đá thế giới) có dạng hình cầu với đường kính khoảng 22cm (H.10.18). Khi bơm căng quả bóng thì thể tích quả bóng bằng bao nhiêu?

Phương pháp giải:
Thể tích hình cầu bán kính R là: \(V = \frac{4}{3}\pi {R^3}\).
Lời giải chi tiết:
Bán kính quả bóng là:
\(R = 22:2 = 11\left( {cm} \right)\)
Thể tích quả bóng là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.11^3} = \frac{{5324}}{3}\pi \left( {c{m^3}} \right)\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 105 SGK Toán 9 Kết nối tri thức
Khinh khí cầu đầu tiên được phát minh bởi anh em nhà Montgolfler (người Pháp) vào năm 1782. Chuyến bay đầu tiên của hai anh em trên khinh khí cầu được thực hiện vào ngày 4 tháng 6 năm 1783 trên bầu trời Place des Cordeliers ở Annonay (nước Pháp) (theo cand.com.vn). Giả sử một khinh khí cầu có dạng hình cầu với đường kính bằng 11m. Tính diện tích mặt khinh khí cầu đó (làm tròn kết quả đến hàng đơn vị của \({m^2}\)).

Phương pháp giải:
+ Tính bán kính khinh khí cầu R.
+ Diện tích mặt khinh khí cầu bán kính R là: \(S = 4\pi {R^2}\).
Lời giải chi tiết:
Bán kính khinh khí cầu là: \(R = \frac{{11}}{2}m\).
Diện tích mặt khinh khí cầu là:
\(S = 4\pi {R^2} = 4\pi .{\left( {\frac{{11}}{2}} \right)^2} = 121\pi \approx 380\left( {{m^2}} \right)\).
Mục 2 của chương trình Toán 9 tập 2 - Kết nối tri thức thường tập trung vào các chủ đề quan trọng như hàm số bậc hai, phương trình bậc hai và ứng dụng của chúng. Việc nắm vững kiến thức nền tảng và phương pháp giải các bài tập trong mục này là vô cùng quan trọng để các em học sinh có thể giải quyết các bài toán phức tạp hơn trong tương lai.
Hàm số bậc hai có dạng y = ax2 + bx + c (a ≠ 0). Để hiểu rõ về hàm số bậc hai, các em cần nắm vững các khái niệm sau:
Phương trình bậc hai có dạng ax2 + bx + c = 0 (a ≠ 0). Các phương pháp giải phương trình bậc hai thường được sử dụng bao gồm:
Hàm số bậc hai và phương trình bậc hai có nhiều ứng dụng trong thực tế, ví dụ như:
Dưới đây là lời giải chi tiết cho các bài tập trong mục 2 trang 103, 104, 105 SGK Toán 9 tập 2 - Kết nối tri thức:
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
Để giải bài tập trong mục 2 một cách hiệu quả, các em cần lưu ý những điều sau:
Hy vọng với những hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập Toán 9 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!