Chào mừng bạn đến với bài học về lý thuyết Hình cầu trong chương trình Toán 9 Kết nối tri thức tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hình cầu, bao gồm định nghĩa, các yếu tố của hình cầu, công thức tính diện tích bề mặt và thể tích.
Chúng tôi cam kết mang đến cho bạn một trải nghiệm học tập hiệu quả và thú vị với các bài giảng được trình bày một cách dễ hiểu, kèm theo nhiều ví dụ minh họa và bài tập thực hành.
Đặc điểm hình cầu Một số yếu tố của hình cầu: Tâm mặt cầu: O. Bán kính mặt cầu: \(R = OB\).
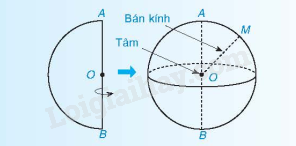
Đặc điểm hình cầu
Một số yếu tố của hình cầu: Tâm mặt cầu: O. Bán kính mặt cầu: \(R = OB\). |
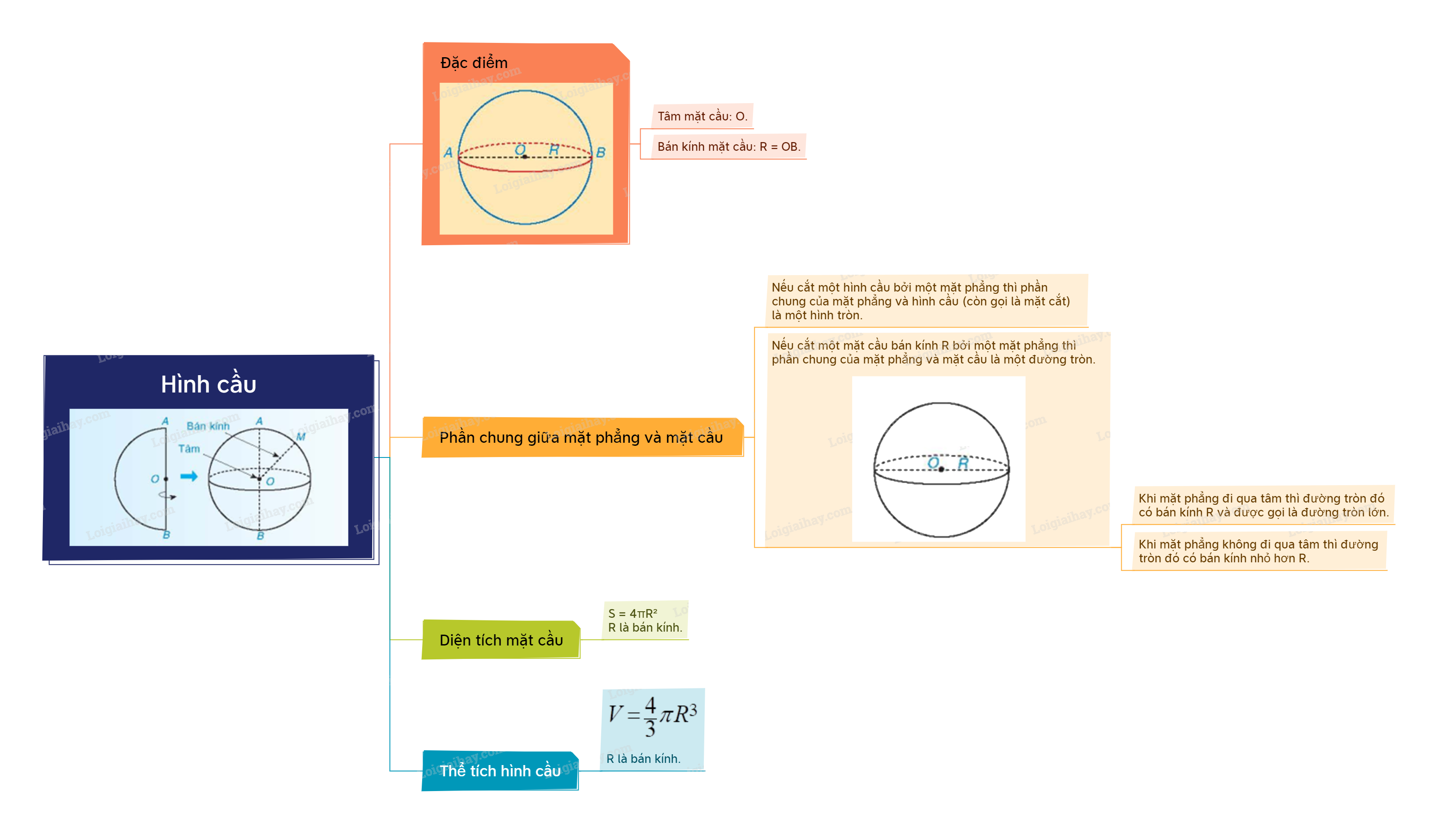
Phần chung giữa mặt phẳng và mặt cầu
1. Nếu cắt một hình cầu bởi một mặt phẳng thì phần chung của mặt phẳng và hình cầu (còn gọi là mặt cắt) là một hình tròn. 2. Nếu cắt một mặt cầu bán kính R bởi một mặt phẳng thì phần chung của mặt phẳng và mặt cầu là một đường tròn.
• Khi mặt phẳng đi qua tâm thì đường tròn đó có bán kính R và được gọi là đường tròn lớn. • Khi mặt phẳng không đi qua tâm thì đường tròn đó có bán kính nhỏ hơn R. |
Diện tích mặt cầu
Công thức tính diện tích mặt cầu: \(S = 4\pi {R^2}\), trong đó R là bán kính. |
Thể tích hình cầu
Công thức tính thể tích hình cầu: \(V = \frac{4}{3}\pi {R^3}\), trong đó R là bán kính. |
Ví dụ:
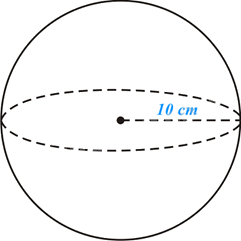
Diện tích mặt cầu là:
\(S = 4\pi {R^2} = 4\pi {.10^2} = 400\pi \left( {c{m^2}} \right)\),
Thể tích hình cầu là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.10^3} = \frac{{4000\pi }}{3}\left( {c{m^3}} \right)\).
Hình cầu là một trong những hình khối quan trọng trong chương trình Hình học lớp 9. Việc nắm vững lý thuyết và các công thức liên quan đến hình cầu là rất cần thiết để giải quyết các bài toán thực tế và chuẩn bị cho các kỳ thi quan trọng.
Hình cầu là tập hợp tất cả các điểm trong không gian cách một điểm cố định (gọi là tâm) một khoảng không đổi (gọi là bán kính).
Diện tích bề mặt của hình cầu được tính theo công thức:
S = 4πR2
Trong đó:
Thể tích của hình cầu được tính theo công thức:
V = (4/3)πR3
Trong đó:
Dưới đây là một số dạng bài tập thường gặp về hình cầu:
Ví dụ 1: Tính diện tích bề mặt của hình cầu có bán kính R = 5cm.
Giải:
Áp dụng công thức S = 4πR2, ta có:
S = 4 * 3.14159 * 52 = 314.159 cm2
Ví dụ 2: Tính thể tích của hình cầu có bán kính R = 3cm.
Giải:
Áp dụng công thức V = (4/3)πR3, ta có:
V = (4/3) * 3.14159 * 33 = 113.097 cm3
Để củng cố kiến thức về lý thuyết Hình cầu, bạn có thể thực hành giải các bài tập sau:
Hy vọng bài học về lý thuyết Hình cầu Toán 9 Kết nối tri thức này đã cung cấp cho bạn những kiến thức cần thiết và hữu ích. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải quyết các bài toán liên quan đến hình cầu.