Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài tập 9.9 trang 76 SGK Toán 9 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về hàm số bậc nhất.
Chúng tôi sẽ cung cấp phương pháp giải bài tập này một cách rõ ràng, từng bước, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC. Chứng minh rằng (widehat {BAH} = widehat {OAC}).
Đề bài
Cho tam giác ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC. Chứng minh rằng \(\widehat {BAH} = \widehat {OAC}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Gọi E là giao điểm của AH và BC. Chứng minh tam giác AEB vuông tại E nên \(\widehat {BAH} + \widehat B = {90^o}\left( 1 \right)\)
+ Gọi AD là đường kính đường tròn (O). Chứng minh tam giác ADC vuông tại C nên \(\widehat {OAC} + \widehat D = {90^o}\left( 2 \right)\)
+ Chứng minh được \(\widehat B = \widehat D\left( 3 \right)\)
+ Từ (1), (2), (3) ta có: \(\widehat {BAH} = \widehat {OAC}\)
Lời giải chi tiết
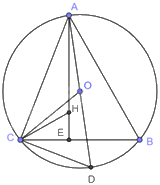
Gọi E là giao điểm của AH và BC nên AE là đường cao của tam giác ABC. Do đó, \(AE \bot BC\)
Suy ra, tam giác BAE vuông tại E nên \(\widehat {EAB} + \widehat B = {90^o}\) hay \(\widehat {BAH} + \widehat B = {90^o}\left( 1 \right)\)
Gọi AD là đường kính của (O). Khi đó, tam giác CAD vuông tại C. Suy ra: \(\widehat {OAC} + \widehat D = {90^o}\left( 2 \right)\)
Vì hai góc B và D là góc nội tiếp cùng chắn cung AC của đường tròn (O; OA) nên \(\widehat B = \widehat D\left( 3 \right)\)
Từ (1), (2) và (3) ta có: \(\widehat {BAH} = \widehat {OAC}\)
Bài tập 9.9 trang 76 SGK Toán 9 tập 2 yêu cầu chúng ta xét hàm số y = (m-1)x + 3. Để hàm số này là hàm số bậc nhất, điều kiện cần và đủ là hệ số của x khác 0, tức là m-1 ≠ 0. Từ đó, ta suy ra m ≠ 1.
Như đã phân tích ở trên, để y = (m-1)x + 3 là hàm số bậc nhất, ta cần m ≠ 1. Điều này có nghĩa là với mọi giá trị của m khác 1, hàm số đều là hàm số bậc nhất.
Hàm số bậc nhất y = ax + b đồng biến khi và chỉ khi a > 0. Trong trường hợp này, a = m-1. Vậy, để hàm số y = (m-1)x + 3 đồng biến, ta cần m-1 > 0, suy ra m > 1.
Hàm số bậc nhất y = ax + b nghịch biến khi và chỉ khi a < 0. Trong trường hợp này, a = m-1. Vậy, để hàm số y = (m-1)x + 3 nghịch biến, ta cần m-1 < 0, suy ra m < 1.
Ví dụ 1: Nếu m = 2, hàm số trở thành y = (2-1)x + 3 = x + 3. Đây là hàm số bậc nhất đồng biến vì hệ số của x là 1 > 0.
Ví dụ 2: Nếu m = 0, hàm số trở thành y = (0-1)x + 3 = -x + 3. Đây là hàm số bậc nhất nghịch biến vì hệ số của x là -1 < 0.
Để củng cố kiến thức, bạn có thể thử giải các bài tập tương tự sau:
Bài tập 9.9 trang 76 SGK Toán 9 tập 2 là một bài tập cơ bản nhưng quan trọng trong chương trình học Toán 9. Việc hiểu rõ điều kiện để hàm số là hàm số bậc nhất và cách xác định tính đồng biến, nghịch biến của hàm số sẽ giúp bạn giải quyết các bài tập phức tạp hơn một cách dễ dàng.
| Điều kiện | Kết quả |
|---|---|
| m ≠ 1 | Hàm số y = (m-1)x + 3 là hàm số bậc nhất |
| m > 1 | Hàm số y = (m-1)x + 3 là hàm số bậc nhất đồng biến |
| m < 1 | Hàm số y = (m-1)x + 3 là hàm số bậc nhất nghịch biến |