Bài tập 9.30 trang 89 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 9.30 trang 89 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
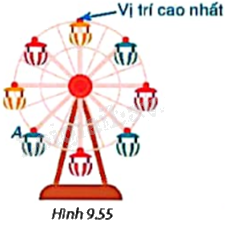
Cho vòng quay mặt trời gồm tám cabin như Hình 9.55. Hỏi để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiều kim đồng hồ quanh tâm bao nhiêu độ?
Đề bài
Cho vòng quay mặt trời gồm tám cabin như Hình 9.55. Hỏi để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiều kim đồng hồ quanh tâm bao nhiêu độ?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Gọi tám cabin tạo thành một bát giác đều BACDEFGH nội tiếp đường tròn (O).
+ Chứng minh \(\Delta HOB = \Delta HOG = \Delta FOG = \Delta FOE = \Delta DOE = \Delta DOC = \Delta AOC = \Delta AOB\left( {c.c.c} \right)\), suy ra: \(\widehat {HOB} = \widehat {HOG} = \widehat {GOF} = \widehat {EOF} = \widehat {DOE} = \widehat {COD} = \widehat {AOC} = \widehat {AOB} = \frac{{{{360}^o}}}{8} = {45^o}\)
+ Tính góc AOG
+ Để cabin A di chuyển đến vị trí cao nhất (vị trí cabin G) thì vòng quay phải quay theo chiều thuận kim đồng hồ quanh tâm góc \({135^o}\).
Lời giải chi tiết
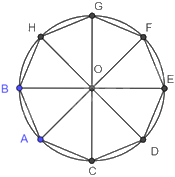
Gọi tám cabin tạo thành một bát giác đều BACDEFGH nội tiếp đường tròn (O).
Vì BACDEFGH là bát giác đều nên
\(AB = AC = CD = DE = EF = FG = GH = HB\)
Vì BACDEFGH là bát giác nội tiếp đường tròn (O) nên
\(OA = OB = OC = OD = OE = OF = OH = OG\)
Do đó
\(\Delta HOB = \Delta HOG = \Delta FOG = \Delta FOE = \Delta DOE = \Delta DOC = \Delta AOC = \Delta AOB\left( {c.c.c} \right)\)
Suy ra
\(\widehat {HOB} = \widehat {HOG} = \widehat {GOF} = \widehat {EOF} = \widehat {DOE} = \widehat {COD} = \widehat {AOC} = \widehat {AOB} = \frac{{{{360}^o}}}{8} = {45^o}\)
Ta có:
\(\widehat {AOG} = \widehat {AOB} + \widehat {BOH} + \widehat {HOG} = {45^o} + {45^o} + {45^o} = {135^o}\)
Để cabin A di chuyển đến vị trí cao nhất (vị trí cabin G) thì vòng quay phải quay theo chiều thuận kim đồng hồ quanh tâm góc \({135^o}\).
Bài tập 9.30 trang 89 SGK Toán 9 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài và phân tích các thông tin đã cho. Xác định rõ các yếu tố liên quan đến hàm số bậc hai, chẳng hạn như các điểm mà đồ thị hàm số đi qua, các điều kiện ràng buộc, hoặc các yêu cầu cụ thể của bài toán.
Sau khi phân tích đề bài, chúng ta cần tìm ra hướng giải phù hợp. Thông thường, để giải các bài toán liên quan đến hàm số bậc hai, chúng ta sẽ sử dụng các phương pháp sau:
(Ở đây sẽ là lời giải chi tiết của bài tập 9.30, bao gồm các bước giải, giải thích rõ ràng và các kết luận chính. Lời giải này sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm vững phương pháp giải.)
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập 9.30, chúng ta sẽ cùng xem xét một số ví dụ minh họa. Các ví dụ này sẽ có cấu trúc tương tự như bài tập 9.30, nhưng có các thông tin khác nhau. Thông qua việc giải các ví dụ này, các em sẽ có cơ hội rèn luyện kỹ năng giải bài tập và tự tin hơn khi đối mặt với các bài toán tương tự.
Sau khi xem xét các ví dụ minh họa, chúng ta sẽ cùng giải một số bài tập tương tự. Các bài tập này sẽ được chọn lọc từ các đề thi và kiểm tra trước đây, đảm bảo tính đa dạng và phong phú. Việc giải các bài tập này sẽ giúp các em củng cố kiến thức và chuẩn bị tốt nhất cho các kỳ thi sắp tới.
Khi giải bài tập về hàm số bậc hai, các em cần lưu ý một số điều sau:
Bài tập 9.30 trang 89 SGK Toán 9 tập 2 là một bài tập quan trọng trong chương trình Toán 9 Kết nối tri thức. Việc nắm vững phương pháp giải bài tập này sẽ giúp các em học sinh tự tin hơn khi đối mặt với các bài toán tương tự trong các kỳ thi và kiểm tra. Hy vọng rằng, với lời giải chi tiết và các ví dụ minh họa mà Giaitoan.edu.vn đã cung cấp, các em sẽ hiểu rõ hơn về bài tập này và đạt được kết quả tốt nhất.
| Công thức | Mô tả |
|---|---|
| y = ax2 + bx + c | Dạng tổng quát của hàm số bậc hai |
| x = -b / 2a | Hoành độ đỉnh của parabol |
| Δ = b2 - 4ac | Biệt thức của phương trình bậc hai |