Giải bài tập 9.20 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức

Bài tập 9.20 trang 83 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.

Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục môn Toán. Chúng tôi cung cấp đầy đủ các bài giải SGK Toán 9, bài tập trắc nghiệm, và các tài liệu học tập hữu ích khác.

Cho hình bình hành ABCD nội tiếp đường tròn (O). Chứng minh rằng ABCD là hình chữ nhật.

Đề bài

Cho hình bình hành ABCD nội tiếp đường tròn (O). Chứng minh rằng ABCD là hình chữ nhật.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 9.20 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức 1

Sử dụng tính chất hai góc đối nhau của hình bình hành bằng nhau và tứ giác nội tiếp có tổng hai góc đối nhau bằng \(180^0\) để chứng minh hình bình hành có một góc vuông là hình chữ nhật.

Lời giải chi tiết

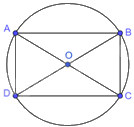
Giải bài tập 9.20 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức 2

Vì ABCD là hình bình hành nên \(\widehat A = \widehat C\).

Mà hình bình hành ABCD nội tiếp đường tròn O nên \(\widehat A + \widehat C = 180^\circ\).

Từ đó, ta có \(\widehat A = \widehat C = \frac{180^\circ}{2} = 90^\circ\).

Hình bình hành ABCD có một góc vuông nên là hình chữ nhật.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 9.20 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức đặc sắc thuộc chuyên mục sách bài tập toán 9 trên nền tảng tài liệu toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 9.20 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức: Hướng dẫn chi tiết

Bài tập 9.20 SGK Toán 9 tập 2 Kết nối tri thức là một bài toán ứng dụng thực tế về hàm số bậc hai. Để giải bài tập này, học sinh cần nắm vững các kiến thức về:

Định nghĩa hàm số bậc hai.
Dạng tổng quát của hàm số bậc hai: y = ax² + bx + c (a ≠ 0).
Hệ số a, b, c và vai trò của chúng trong việc xác định tính chất của parabol.
Đỉnh của parabol và cách tìm tọa độ đỉnh.
Trục đối xứng của parabol.
Bảng giá trị của hàm số bậc hai.
Ứng dụng của hàm số bậc hai trong việc giải quyết các bài toán thực tế.

Nội dung bài tập 9.20 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức

Bài tập 9.20 yêu cầu học sinh giải một bài toán liên quan đến việc xác định phương trình của một parabol đi qua ba điểm cho trước. Bài toán thường được trình bày dưới dạng một tình huống thực tế, ví dụ như việc xác định quỹ đạo của một vật được ném lên không trung.

Phương pháp giải bài tập 9.20 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức

Để giải bài tập này, học sinh có thể áp dụng các bước sau:

Bước 1: Gọi phương trình của parabol có dạng y = ax² + bx + c.
Bước 2: Thay tọa độ của ba điểm mà parabol đi qua vào phương trình để được ba phương trình.
Bước 3: Giải hệ ba phương trình này để tìm các hệ số a, b, c.
Bước 4: Thay các giá trị a, b, c vừa tìm được vào phương trình y = ax² + bx + c để được phương trình của parabol.

Ví dụ minh họa giải bài tập 9.20 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức

Giả sử bài toán yêu cầu tìm phương trình của parabol đi qua ba điểm A(0; 1), B(1; 2), và C(-1; 0). Ta thực hiện các bước sau:

Gọi phương trình của parabol có dạng y = ax² + bx + c.
Thay tọa độ của các điểm A, B, C vào phương trình, ta được hệ phương trình sau:
- 1 = a(0)² + b(0) + c
- 2 = a(1)² + b(1) + c
- 0 = a(-1)² + b(-1) + c
Giải hệ phương trình này, ta được a = 1/2, b = 1/2, c = 1.
Vậy phương trình của parabol là y = (1/2)x² + (1/2)x + 1.

Lưu ý khi giải bài tập 9.20 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức

Khi giải bài tập này, học sinh cần lưu ý một số điểm sau:

Đảm bảo rằng các điểm cho trước không thẳng hàng. Nếu ba điểm thẳng hàng, thì không tồn tại parabol đi qua cả ba điểm đó.
Kiểm tra lại kết quả bằng cách thay tọa độ của các điểm đã cho vào phương trình parabol vừa tìm được.
Sử dụng máy tính bỏ túi để giải hệ phương trình một cách nhanh chóng và chính xác.

Bài tập tương tự và luyện tập

Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc hai, học sinh có thể làm thêm các bài tập tương tự trong SGK Toán 9 tập 2 Kết nối tri thức và các tài liệu luyện tập khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.

Kết luận

Bài tập 9.20 trang 83 SGK Toán 9 tập 2 Kết nối tri thức là một bài toán quan trọng giúp học sinh hiểu sâu hơn về hàm số bậc hai và ứng dụng của nó trong thực tế. Hy vọng rằng với hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, các em học sinh sẽ có thể tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.