Bài tập 5.2 trang 86 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và làm bài tập hiệu quả.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 9 tập 1 Kết nối tri thức, đảm bảo hỗ trợ tối đa cho quá trình học tập của các em.
Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Chứng minh rằng các điểm A, B, C thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.
Đề bài
Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Chứng minh rằng các điểm A, B, C thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Từ định lý Pythagore tính được độ dài cạnh BC.
- Từ tính chất đường trung tuyến trong tam giác vuông suy ra A, B, C thuộc đường tròn đường kính BC.
Lời giải chi tiết
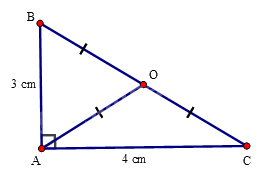
Áp dụng định lý Pythagore ta có: \(B{C^2} = A{B^2} + A{C^2} = {3^2} + {4^2} = 25 \Rightarrow BC = 5\)(cm)
Gọi O là trung điểm của cạnh BC.
Ta có AO là trung tuyến ứng với cạnh huyền nên \(OA = \frac{{BC}}{2} = OB = OC = 2,5\)(cm).
Suy ra A, B, C cùng thuộc đường tròn bán kính OB = 2,5 cm.
Bài tập 5.2 trang 86 SGK Toán 9 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương Hàm số bậc nhất. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về hàm số bậc nhất, cách xác định hàm số, và cách vẽ đồ thị hàm số. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Cho hàm số y = (m-1)x + 3. Tìm giá trị của m để hàm số đồng biến.
Để hàm số y = (m-1)x + 3 đồng biến, hệ số của x phải lớn hơn 0. Tức là:
m - 1 > 0
Suy ra:
m > 1
Vậy, để hàm số y = (m-1)x + 3 đồng biến thì m > 1.
Bài toán này kiểm tra khả năng vận dụng kiến thức về tính chất của hàm số bậc nhất. Một hàm số bậc nhất y = ax + b được gọi là đồng biến nếu a > 0 và nghịch biến nếu a < 0. Trong bài toán này, chúng ta cần xác định điều kiện để hệ số a (tức là m-1) lớn hơn 0.
Ngoài bài tập 5.2, còn rất nhiều bài tập tương tự liên quan đến hàm số bậc nhất. Một số dạng bài tập thường gặp bao gồm:
Để giải các bài tập này, học sinh cần nắm vững các khái niệm cơ bản về hàm số bậc nhất, cách xác định hàm số, và cách vẽ đồ thị hàm số. Ngoài ra, cần luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế. Ví dụ, trong kinh tế, hàm số bậc nhất có thể được sử dụng để mô tả mối quan hệ giữa chi phí và sản lượng. Trong vật lý, hàm số bậc nhất có thể được sử dụng để mô tả mối quan hệ giữa quãng đường và thời gian khi vật chuyển động đều. Việc hiểu rõ về hàm số bậc nhất giúp chúng ta giải quyết các bài toán thực tế một cách hiệu quả.
Để củng cố kiến thức về hàm số bậc nhất, các em có thể tự giải các bài tập sau:
Bài tập 5.2 trang 86 SGK Toán 9 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về tính chất của hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ nắm vững kiến thức và làm bài tập hiệu quả. Chúc các em học tốt!