Giải bài tập 9.15 trang 79 SGK Toán 9 tập 2 - Kết nối tri thức

Bài tập 9.15 trang 79 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 9.15 trang 79 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.

Cho tam giác đều ABC có cạnh bằng 3cm và nội tiếp đường tròn (O) như Hình 9.26. a) Tính bán kính R của đường tròn (O). b) Tính diện tích hình viên phân giới hạn bởi dây cung BC và cung nhỏ BC.

Đề bài

Cho tam giác đều ABC có cạnh bằng 3cm và nội tiếp đường tròn (O) như Hình 9.26.

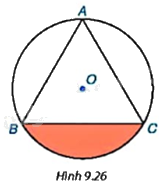
Giải bài tập 9.15 trang 79 SGK Toán 9 tập 2 - Kết nối tri thức 1

a) Tính bán kính R của đường tròn (O).

b) Tính diện tích hình viên phân giới hạn bởi dây cung BC và cung nhỏ BC.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 9.15 trang 79 SGK Toán 9 tập 2 - Kết nối tri thức 2

a) Dựa vào công thức tính bán kính đường tròn ngoại tiếp tam giác: $R = \frac{\sqrt 3}{3}$.độ dài cạnh

b) + Tính ${S_1}$ là diện tích hình quạt tròn BOC, tính diện tích tam giác BOC.

+ Khi đó, S_{viên phân}$ = {S_1} - {S_{BOC}}$.

Lời giải chi tiết

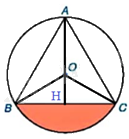
Giải bài tập 9.15 trang 79 SGK Toán 9 tập 2 - Kết nối tri thức 3

a) Bán kính R của đường tròn O ngoại tiếp tam giác đều ABC là:

$R = \frac{\sqrt 3}{3}.3 = \sqrt 3 \left( {cm} \right)$

b) Vì tam giác ABC đều nên $\widehat{BAC} = 60^o$

Vì $\widehat{BOC}$ là góc ở tâm chắn cung BC, $\widehat{BAC}$ là góc nội tiếp chắn cung BC nên $\widehat{BOC}=2\widehat{BAC} = 2.{60}^{o} ={{120}^{o}}$

Diện tích hình quạt tròn BOC là:

${S_1} = \frac{{120}}{{360}}.\pi .{\left( {\sqrt 3 } \right)^2} = \pi \left( {c{m^2}} \right)$

Vì ΔABC đều nên tâm O của đường tròn ngoại tiếp ΔABC đồng thời là trọng tâm, trực tâm của tam giác.

Vẽ đường cao AH của tam giác ABC đều nên AH vừa là đường cao, vừa là đường trung tuyến, vừa là đường trung trực của tam giác ABC.

Vì O là trọng tâm nên $OH = \frac{AO}{2} = \frac{\sqrt 3}{2} (cm)$

Diện tích tam giác BOC là:

${S_{BOC}} = \frac{1}{2}OH.BC = \frac{1}{2}.\frac{{\sqrt 3 }}{2}.3 = \frac{{3\sqrt 3 }}{4}\left( {c{m^2}} \right)$

Diện tích hình viên phân giới hạn bởi dây cung BC và cung nhỏ BC là:

S_{viên phân}$ = {S_1} - {S_{BOC}} = \pi - \frac{{3\sqrt 3 }}{4}\left( {c{m^2}} \right)$

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 9.15 trang 79 SGK Toán 9 tập 2 - Kết nối tri thức đặc sắc thuộc chuyên mục toán 9 trên nền tảng tài liệu toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 9.15 trang 79 SGK Toán 9 tập 2 - Kết nối tri thức: Hướng dẫn chi tiết

Bài tập 9.15 trang 79 SGK Toán 9 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:

Hàm số bậc hai: Định nghĩa, dạng tổng quát, đồ thị, tính chất.
Cách xác định hệ số a, b, c của hàm số bậc hai.
Cách tìm hoành độ giao điểm của đồ thị hàm số với trục hoành.
Cách tìm tọa độ đỉnh của parabol.
Ứng dụng của hàm số bậc hai trong giải quyết các bài toán thực tế.

Đề bài: (Đề bài cụ thể của bài tập 9.15 sẽ được chèn vào đây. Ví dụ: Một quả bóng được ném lên từ mặt đất với vận tốc ban đầu là 15 m/s. Hãy viết phương trình mô tả quỹ đạo của quả bóng và tìm độ cao lớn nhất mà quả bóng đạt được.)

Lời giải:

Xác định hệ tọa độ: Chọn gốc tọa độ tại vị trí ném bóng, trục Ox hướng ngang, trục Oy hướng thẳng đứng.
Xây dựng phương trình: Quỹ đạo của quả bóng là một parabol có phương trình dạng y = ax² + bx + c. Trong trường hợp này, a = -5 (do trọng lực), b = 0 (vì không có lực tác dụng theo phương ngang), và c = 0 (vì quả bóng được ném từ mặt đất). Vậy phương trình quỹ đạo là y = -5x² + 15x.
Tìm độ cao lớn nhất: Độ cao lớn nhất mà quả bóng đạt được là tung độ của đỉnh parabol. Hoành độ đỉnh của parabol là x = -b / (2a) = -0 / (2 * -5) = 0. Thay x = 0 vào phương trình, ta được y = -5 * 0² + 15 * 0 = 0. (Lưu ý: Đây là một ví dụ đơn giản, đề bài thực tế có thể phức tạp hơn và cần tính toán khác.)
Kết luận: (Kết luận dựa trên kết quả tính toán.)

Lưu ý:

Khi giải các bài toán liên quan đến hàm số bậc hai, cần chú ý đến đơn vị đo lường và đảm bảo tính chính xác của các phép tính.
Nên vẽ đồ thị hàm số để hình dung rõ hơn về quỹ đạo của vật thể.
Thực hành giải nhiều bài tập tương tự để nắm vững phương pháp và kỹ năng giải toán.

Các dạng bài tập tương tự

Ngoài bài tập 9.15, SGK Toán 9 tập 2 Kết nối tri thức còn nhiều bài tập khác liên quan đến hàm số bậc hai. Dưới đây là một số dạng bài tập thường gặp:

Tìm hệ số của hàm số bậc hai khi biết các thông tin về đồ thị.
Xác định khoảng đồng biến, nghịch biến của hàm số.
Giải phương trình bậc hai.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số.
Ứng dụng hàm số bậc hai trong các bài toán hình học.

Giaitoan.edu.vn sẽ tiếp tục cập nhật và cung cấp lời giải chi tiết cho các bài tập khác trong chương trình Toán 9 Kết nối tri thức. Hãy truy cập website của chúng tôi để học toán online hiệu quả và đạt kết quả cao trong học tập!

Bảng tóm tắt kiến thức về hàm số bậc hai

Khái niệm	Công thức
Dạng tổng quát	y = ax² + bx + c (a ≠ 0)
Hoành độ đỉnh	x = -b / (2a)
Tung độ đỉnh	y = -Δ / (4a)
Delta (Δ)	Δ = b² - 4ac

Hy vọng với lời giải chi tiết và những kiến thức bổ ích trên, các em học sinh sẽ tự tin hơn khi giải bài tập 9.15 trang 79 SGK Toán 9 tập 2 - Kết nối tri thức và các bài tập tương tự. Chúc các em học tốt!