Bài tập 5.30 trang 110 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Đây là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 5.30 này, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho đường tròn (O) đường kính AB, tiếp tuyến xx’ tại A và tiếp tuyến yy’ tại B của (O). Một tiếp tuyến thứ ba của (O) tại điểm P (khác A và B) cắt xx’ tại M và cắt yy’ tại N. a) Chứng minh rằng MN = MA + NB. b) Đường thẳng đi qua O và vuông góc với AB cắt NM tại Q. Chứng minh rằng Q là trung điểm của đoạn MN. c) Chứng minh rằng AB tiếp xúc với đường tròn đường kính MN.
Đề bài
Cho đường tròn (O) đường kính AB, tiếp tuyến xx’ tại A và tiếp tuyến yy’ tại B của (O). Một tiếp tuyến thứ ba của (O) tại điểm P (khác A và B) cắt xx’ tại M và cắt yy’ tại N.
a) Chứng minh rằng MN = MA + NB.
b) Đường thẳng đi qua O và vuông góc với AB cắt NM tại Q. Chứng minh rằng Q là trung điểm của đoạn MN.
c) Chứng minh rằng AB tiếp xúc với đường tròn đường kính MN.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Áp dụng tính chất của hai tiếp tuyến cắt nhau.
b) Gọi K là giao điểm của AN và OQ, áp dụng tính chất đường trung bình cho hai tam giác ABN và AMN.
c) Áp dụng tính chất đường trung bình và câu a suy ra
\({\rm{OQ}} = \frac{1}{2}{\rm{MN}}\)nên O thuộc đường tròn đường kính MN, từ đó ta có AB là tiếp tuyến tại M.
Lời giải chi tiết
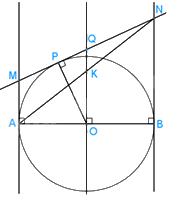
a) MA và MP là hai tiếp tuyến cắt nhau của (O) nên MA = MP
NB và NP là hai tiếp tuyến cắt nhau của (O) nên NB = NP
Ta có: MN = MP + NP = MA + NB
b) Gọi K là giao điểm của AN và OQ.
Ta có: \({\rm{BN//OK}}\) (vì cùng vuông góc với AB) và O là trung điểm của AB.
Suy ra OK là đường trung bình của tam giác ABN.
Do đó K là trung điểm của AN.
Lại có: \({\rm{AM//QK}}\) (vì cùng vuông góc với AB) và K là trung điểm của AN.
Suy ra QK là đường trung bình của tam giác AMN.
Do đó Q là trung điểm của MN.
c) OK là đường trung bình của tam giác ABN nên \({\rm{OK}} = \frac{1}{2}{\rm{NB}}\)
QK là đường trung bình của tam giác AMN nên \({\rm{QK}} = \frac{1}{2}{\rm{MA}}\)
Suy ra: \({\rm{OQ}} = {\rm{OK}} + {\rm{QK}} = \frac{1}{2}{\rm{NB}} + \frac{1}{2}{\rm{MA}} = \frac{1}{2}{\rm{MN}}\)
hay \({\rm{OQ}} = {\rm{AQ}} = {\rm{BQ}}\)
Do đó O thuộc đường tròn đường kính MN.
Mà OQ vuông góc với AB tại O nên AB là tiếp của đường tròn đường kính MN.
Bài tập 5.30 trang 110 SGK Toán 9 tập 1 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết một bài toán thực tế liên quan đến việc xác định hàm số và tính giá trị của hàm số tại một điểm cho trước. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản sau:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hàm số y = 2x + 3. Tính giá trị của y khi x = -1.)
Lời giải:
Ngoài bài tập 5.30, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Để nắm vững kiến thức về hàm số bậc nhất, học sinh nên:
Ví dụ 1: Xác định hàm số y = ax + b biết đồ thị của hàm số đi qua hai điểm A(1; 2) và B(-1; 0).
Lời giải: Thay tọa độ của hai điểm A và B vào phương trình y = ax + b, ta được hệ phương trình:
a + b = 2
-a + b = 0
Giải hệ phương trình này, ta được a = 1 và b = 1. Vậy hàm số cần tìm là y = x + 1.
Bài tập 5.30 trang 110 SGK Toán 9 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự. Chúc các em học tập tốt!