Bài viết này cung cấp lý thuyết đầy đủ và chi tiết về khái niệm phương trình, nghiệm của phương trình, và hệ hai phương trình bậc nhất hai ẩn, theo chương trình Toán 9 Kết nối tri thức. Chúng tôi sẽ giúp bạn hiểu rõ các định nghĩa, tính chất và cách nhận biết các loại phương trình và hệ phương trình này.
Với phương pháp trình bày dễ hiểu, kèm theo các ví dụ minh họa, bạn sẽ dễ dàng nắm bắt kiến thức và áp dụng vào giải các bài tập thực tế. Hãy cùng giaitoan.edu.vn khám phá thế giới của phương trình và hệ phương trình!
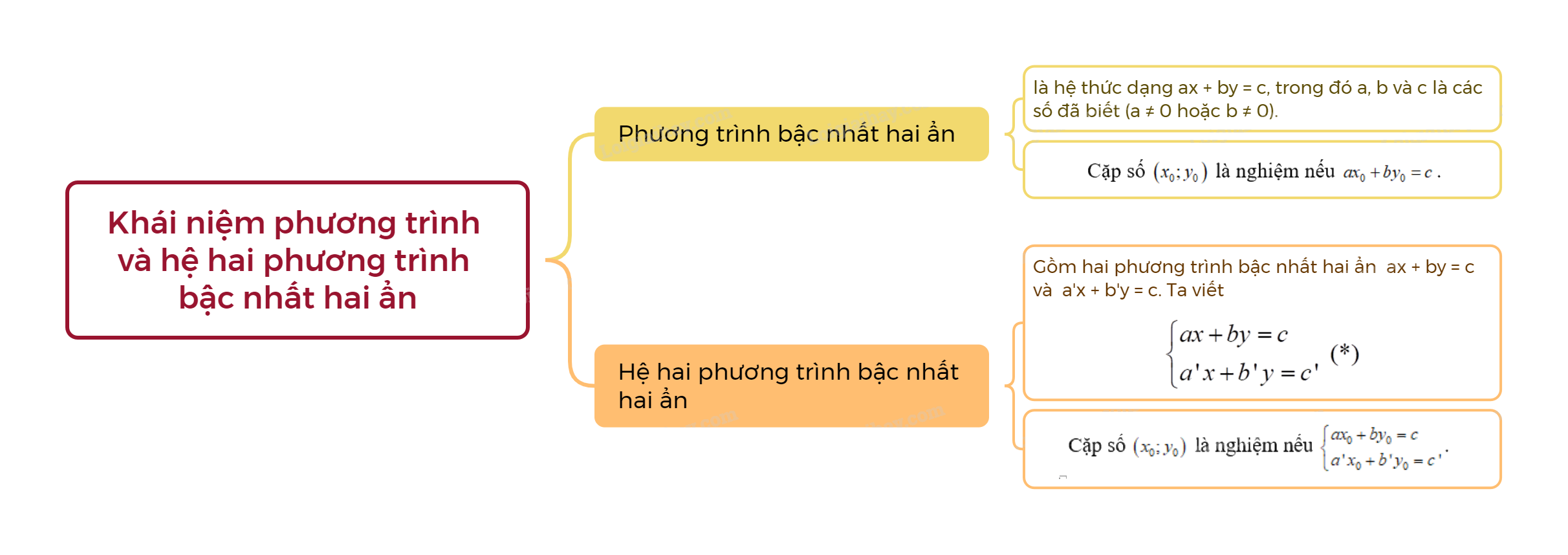
1. Phương trình bậc nhất hai ẩn Khái niệm phương trình bậc nhất hai ẩn
1. Phương trình bậc nhất hai ẩn
Khái niệm phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn x và y là hệ thức dạng \(ax + by = c\), (1) trong đó a, b và c là các số đã biết (\(a \ne 0\) hoặc \(b \ne 0\)). |
Ví dụ: \(2x + 3y = 4\), \(0x + 2y = 3\), \(x + 0y = 2\) là các phương trình bậc nhất hai ẩn.
Nghiệm của phương trình bậc nhất hai ẩn
Nếu tại \(x = {x_0}\) và \(y = {y_0}\) ta có \(a{x_0} + b{y_0} = c\) là một khẳng định đúng thì cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là một nghiệm của phương trình (1). |
Ví dụ: Cặp số \(( - 1;2)\) là nghiệm của phương trình \(2x + 3y = 4\) vì \(2.\left( { - 1} \right) + 3.2 = - 2 + 6 = 4\).
Cặp số \((1;2)\) không là nghiệm của phương trình \(2x + 3y = 4\) vì
\(2.1 + 3.2 = 2 + 6 = 8 \ne 4\).
2. Hệ hai phương trình bậc nhất hai ẩn
Khái niệm hệ hai phương trình bậc nhất hai ẩn
Một cặp gồm hai phương trình bậc nhất hai ẩn \(ax + by = c\) và \(a'x + b'y = c'\) được gọi là một hệ hai phương trình bậc nhất hai ẩn. Ta thường viết hệ phương trình đó dưới dạng: \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\,\,\,(*)\) |
Ví dụ: Hệ phương trình \(\left\{ \begin{array}{l}2x - y = 0\\x + y = 3\end{array} \right.\), \(\left\{ \begin{array}{l}3x = 1\\x - y = 3\end{array} \right.\), \(\left\{ \begin{array}{l}4x - y = 3\\3y = 6\end{array} \right.\) là các hệ phương trình bậc nhất hai ẩn.
Nghiệm của hệ hai phương trình bậc nhất hai ẩn
Mỗi cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là một nghiệm của hệ (*) nếu nó là nghiệm chung của hai phương trình của hệ (*). |
Ví dụ: Cặp số (1; 2) là một nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x - y = 0\\x + y = 3\end{array} \right.\), vì:
\(2x - y = 2.1 - 2 = 0\) nên (1; 2) là nghiệm của phương trình thứ nhất.
\(x + y = 1 + 2 = 3\) nên (1; 2) là nghiệm của phương trình thứ hai.
Trong chương trình Toán 9 Kết nối tri thức, việc nắm vững khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn là nền tảng quan trọng để giải quyết các bài toán đại số. Bài viết này sẽ trình bày chi tiết lý thuyết, ví dụ minh họa và các bài tập áp dụng để giúp học sinh hiểu rõ và nắm vững kiến thức này.
Định nghĩa: Phương trình là một đẳng thức chứa ẩn. Ví dụ: 2x + 3 = 7 là một phương trình với ẩn x.
Nghiệm của phương trình: Nghiệm của phương trình là giá trị của ẩn thay vào phương trình mà hai vế của phương trình bằng nhau. Ví dụ, x = 2 là nghiệm của phương trình 2x + 3 = 7.
Cách giải phương trình: Để giải phương trình, ta thực hiện các phép biến đổi tương đương để đưa phương trình về dạng x = a, với a là một số cụ thể. Các phép biến đổi tương đương bao gồm:
Định nghĩa: Hệ hai phương trình bậc nhất hai ẩn là một tập hợp gồm hai phương trình bậc nhất hai ẩn, có dạng:
ax + by = c
a'x + b'y = c'
Trong đó a, b, a', b', c, c' là các số đã biết, x và y là các ẩn số.
Nghiệm của hệ phương trình: Nghiệm của hệ phương trình là giá trị của x và y sao cho khi thay vào cả hai phương trình của hệ, hai phương trình đều được nghiệm đúng.
Có nhiều phương pháp để giải hệ phương trình bậc nhất hai ẩn, trong đó phổ biến nhất là:
Ví dụ 1: Giải phương trình 3x - 5 = 7
Ta có: 3x - 5 = 7
=> 3x = 12
=> x = 4
Vậy nghiệm của phương trình là x = 4.
Ví dụ 2: Giải hệ phương trình sau:
x + y = 5
2x - y = 1
Sử dụng phương pháp cộng đại số, ta có:
(x + y) + (2x - y) = 5 + 1
=> 3x = 6
=> x = 2
Thay x = 2 vào phương trình x + y = 5, ta có:
2 + y = 5
=> y = 3
Vậy nghiệm của hệ phương trình là x = 2, y = 3.
Giải các phương trình và hệ phương trình sau:
Việc hiểu rõ khái niệm phương trình, nghiệm của phương trình và hệ hai phương trình bậc nhất hai ẩn là rất quan trọng trong chương trình Toán 9 Kết nối tri thức. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết để giải quyết các bài toán liên quan đến chủ đề này. Hãy luyện tập thường xuyên để nắm vững kiến thức và nâng cao kỹ năng giải toán của mình.