Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong sách giáo khoa Toán 9 tập 2 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt nhất trong môn Toán.
Cho tam giác ABC có ba đường phân giác đồng quy tại điểm I. Gọi D, E, F lần lượt là chân các đường vuông góc kẻ từ I xuống các cạnh BC, CA và AB (H.9.19). a) Hãy giải thích vì sao các điểm D, E, F cùng nằm trên một đường tròn có tâm I. b) Gọi (I) là đường tròn trên. Hãy giải thích vì sao (I) tiếp xúc với các cạnh của tam giác ABC.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 6 trang 75SGK Toán 9 Kết nối tri thức
Cho tam giác ABC đều có trọng tâm G.
a) Giải thích vì sao G cũng là tâm đường tròn nội tiếp tam giác ABC.
b) Từ đó, giải thích vì sao bán kính đường tròn nội tiếp tam giác ABC bằng một nửa đường tròn ngoại tiếp tam giác ABC và bằng \(\frac{{\sqrt 3 }}{6}BC\).
Phương pháp giải:
a) Sử dụng tính chất: Trong tam giác đều, trọng tâm đồng thời là giao điểm của ba đường phân giác. Suy ra, G là tâm đường tròn nội tiếp tam giác ABC.
b) + Gọi D là giao điểm của AG và CB. Khi đó, GD là bán kính đường tròn đường tròn nội tiếp tam giác ABC, AG là bán kính đường tròn ngoại tiếp tam giác ABC.
+ Theo tính chất của trọng tâm trong tam giác ABC ta có: \(GD = \frac{1}{2}AG = \frac{1}{3}AD\).
+ Dựa vào kiến thức bán kính của đường tròn ngoại tiếp bằng \(\frac{\sqrt 3}{3}\) lần độ dài cạnh để tính bán kính đường tròn nội tiếp.
Lời giải chi tiết:
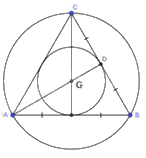
a) Tam giác ABC đều nên G là trọng tâm của tam giác ABC đồng thời là giao điểm của ba đường phân giác. Do đó, G là tâm đường tròn nội tiếp tam giác ABC.
b) Vì G là giao điểm của ba đường trung trực trong tam giác đều ABC (do G là trọng tâm tam giác ABC) nên G là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi D là giao điểm của AG và CB. Suy ra, AG là bán kính đường tròn ngoại tiếp tam giác ABC.
Tam giác ABC đều nên AD là đường trung tuyến đồng thời là đường cao trong tam giác. Do đó, \(GD \bot CB\) tại D. Suy ra, GD là bán kính đường tròn nội tiếp tam giác ABC.
Vì G là trọng tâm tam giác ABC nên \(AG = 2GD\) suy ra \(GD = \frac{1}{2}AG\).
Bán kính đường tròn ngoại tiếp tam giác ABC là: \(AG = \frac{\sqrt 3}{3} BC\)
Do đó, \(GD = \frac{1}{2}.\frac{\sqrt 3}{3} BC = \frac{{\sqrt 3 }}{6}BC\).
Vậy bán kính đường tròn nội tiếp tam giác ABC bằng một nửa đường tròn ngoại tiếp tam giác ABC và bằng \(\frac{{\sqrt 3 }}{6}BC\).
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 75SGK Toán 9 Kết nối tri thức
Mỗi tam giác có bao nhiêu đường tròn nội tiếp? Có bao nhiêu tam giác cùng ngoại tiếp một đường tròn?
Phương pháp giải:
Mỗi tam giác có một đường tròn nội tiếp. Có một tam giác ngoại tiếp một đường tròn.
Lời giải chi tiết:
Mỗi tam giác có một đường tròn nội tiếp.
Có vô số tam giác cùng ngoại tiếp một đường tròn (lấy ba điểm trên đường tròn và vẽ ba tiếp tuyến của đường tròn tại ba điểm đó sao cho các tiếp tuyến cắt nhau tại ba điểm lập thành ba đỉnh của một tam giác, tam giác đó ngoại tiếp đường tròn).
Ví dụ:
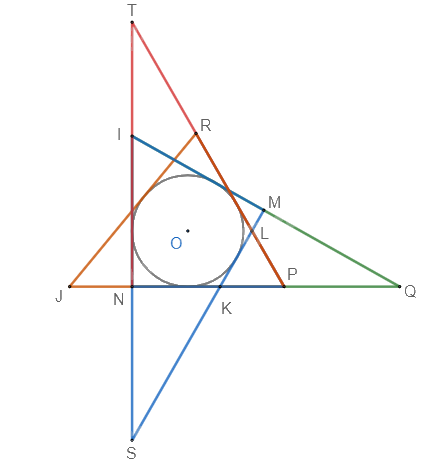
Các tam giác NPT, INQ, JPR, IMS cùng nội tiếp đường tròn O. Ta có thể vẽ nhiều hơn các tam giác ngoại tiếp đường tròn O này.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 5 trang 74SGK Toán 9 Kết nối tri thức
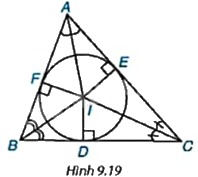
Cho tam giác ABC có ba đường phân giác đồng quy tại điểm I. Gọi D, E, F lần lượt là chân các đường vuông góc kẻ từ I xuống các cạnh BC, CA và AB (H.9.19).
a) Hãy giải thích vì sao các điểm D, E, F cùng nằm trên một đường tròn có tâm I.
b) Gọi (I) là đường tròn trên. Hãy giải thích vì sao (I) tiếp xúc với các cạnh của tam giác ABC.
Phương pháp giải:
a) Sử dụng tính chất: Giao điểm của ba đường phân giác trong tam giác cách đều ba cạnh của tam giác, do đó \(IE = ID = FI\).
b) Vì \(IE \bot AC\left( {E \in AC} \right),IE = R\) nên AC tiếp xúc với đường tròn (I; R) tại E, tương tự ta chứng minh được đường tròn (I) tiếp xúc với các cạnh của tam giác ABC.
Lời giải chi tiết:
a) Vì D, E, F lần lượt là chân các đường vuông góc kẻ từ I xuống các cạnh BC, CA và AB nên \(IF \bot AB,IE \bot AC,ID \bot BC\).
Vì I là giao điểm của ba đường phân giác nên I cách đều ba cạnh AB, AC, CB. Do đó, \(IE = IF = ID\)
Do đó, ba điểm D, E, F cùng nằm trên một đường tròn có tâm I.
b) Gọi \(IE = IF = ID = R\) nên ba điểm D, E, F cùng nằm trên đường tròn (I; R).
Vì \(IE \bot AC\left( {E \in AC} \right),IE = R\) nên AC tiếp xúc với đường tròn (I; R) tại E.
Vì \(IF \bot AB\left( {F \in AB} \right),IF = R\) nên AB tiếp xúc với đường tròn (I; R) tại F.
Vì \(ID \bot BC\left( {D \in BC} \right),ID = R\) nên BC tiếp xúc với đường tròn (I; R) tại D.
Vậy đường tròn (I) ở trên tiếp xúc với các cạnh của tam giác ABC.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 76SGK Toán 9 Kết nối tri thức
Cho tam giác đều ABC (H.9.22).
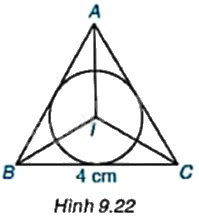
a) Vẽ đường tròn (I; r) nội tiếp tam giác ABC.
b) Biết rằng \(BC = 4cm\), hãy tính bán kính r.
Phương pháp giải:
a) + Vẽ ba đường phân giác của tam giác ABC.
+ Gọi I là giao điểm của ba đường phân giác đó.
+ Gọi H là giao điểm của AI và BC. Vẽ đường tròn tâm I, bán kính IH.
+ Khi đó, đường tròn (I; IH) là đường tròn nội tiếp tam giác ABC cần vẽ.
b) Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\)
Lời giải chi tiết:
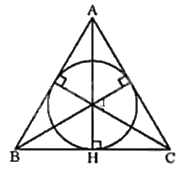
a) Vẽ ba đường phân giác của tam giác ABC. Gọi I là giao điểm của ba đường phân giác đó.
Gọi H là giao điểm của AI và BC. Vẽ đường tròn tâm I, bán kính IH.
Khi đó, đường tròn (I; IH) là đường tròn nội tiếp tam giác ABC cần vẽ.
b) Vì (I; r) nội tiếp tam giác ABC nên bán kính đường tròn nội tiếp tam giác ABC là:
\(r = \frac{{BC\sqrt 3 }}{6} = \frac{{4\sqrt 3 }}{6} = \frac{{2\sqrt 3 }}{3}\left( {cm} \right)\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 5 trang 74SGK Toán 9 Kết nối tri thức
Cho tam giác ABC có ba đường phân giác đồng quy tại điểm I. Gọi D, E, F lần lượt là chân các đường vuông góc kẻ từ I xuống các cạnh BC, CA và AB (H.9.19).
a) Hãy giải thích vì sao các điểm D, E, F cùng nằm trên một đường tròn có tâm I.
b) Gọi (I) là đường tròn trên. Hãy giải thích vì sao (I) tiếp xúc với các cạnh của tam giác ABC.
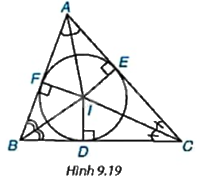
Phương pháp giải:
a) Sử dụng tính chất: Giao điểm của ba đường phân giác trong tam giác cách đều ba cạnh của tam giác, do đó \(IE = ID = FI\).
b) Vì \(IE \bot AC\left( {E \in AC} \right),IE = R\) nên AC tiếp xúc với đường tròn (I; R) tại E, tương tự ta chứng minh được đường tròn (I) tiếp xúc với các cạnh của tam giác ABC.
Lời giải chi tiết:
a) Vì D, E, F lần lượt là chân các đường vuông góc kẻ từ I xuống các cạnh BC, CA và AB nên \(IF \bot AB,IE \bot AC,ID \bot BC\).
Vì I là giao điểm của ba đường phân giác nên I cách đều ba cạnh AB, AC, CB. Do đó, \(IE = IF = ID\)
Do đó, ba điểm D, E, F cùng nằm trên một đường tròn có tâm I.
b) Gọi \(IE = IF = ID = R\) nên ba điểm D, E, F cùng nằm trên đường tròn (I; R).
Vì \(IE \bot AC\left( {E \in AC} \right),IE = R\) nên AC tiếp xúc với đường tròn (I; R) tại E.
Vì \(IF \bot AB\left( {F \in AB} \right),IF = R\) nên AB tiếp xúc với đường tròn (I; R) tại F.
Vì \(ID \bot BC\left( {D \in BC} \right),ID = R\) nên BC tiếp xúc với đường tròn (I; R) tại D.
Vậy đường tròn (I) ở trên tiếp xúc với các cạnh của tam giác ABC.
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 75SGK Toán 9 Kết nối tri thức
Mỗi tam giác có bao nhiêu đường tròn nội tiếp? Có bao nhiêu tam giác cùng ngoại tiếp một đường tròn?
Phương pháp giải:
Mỗi tam giác có một đường tròn nội tiếp. Có một tam giác ngoại tiếp một đường tròn.
Lời giải chi tiết:
Mỗi tam giác có một đường tròn nội tiếp.
Có vô số tam giác cùng ngoại tiếp một đường tròn (lấy ba điểm trên đường tròn và vẽ ba tiếp tuyến của đường tròn tại ba điểm đó sao cho các tiếp tuyến cắt nhau tại ba điểm lập thành ba đỉnh của một tam giác, tam giác đó ngoại tiếp đường tròn).
Ví dụ:
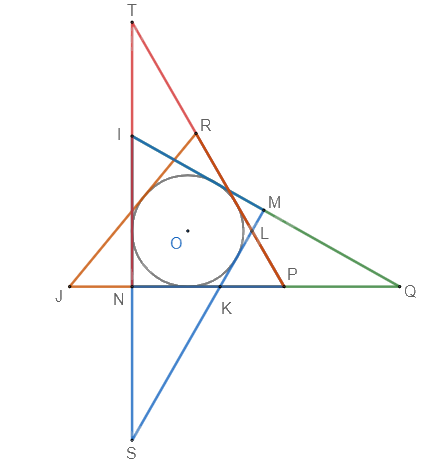
Các tam giác NPT, INQ, JPR, IMS cùng nội tiếp đường tròn O. Ta có thể vẽ nhiều hơn các tam giác ngoại tiếp đường tròn O này.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 6 trang 75SGK Toán 9 Kết nối tri thức
Cho tam giác ABC đều có trọng tâm G.
a) Giải thích vì sao G cũng là tâm đường tròn nội tiếp tam giác ABC.
b) Từ đó, giải thích vì sao bán kính đường tròn nội tiếp tam giác ABC bằng một nửa đường tròn ngoại tiếp tam giác ABC và bằng \(\frac{{\sqrt 3 }}{6}BC\).
Phương pháp giải:
a) Sử dụng tính chất: Trong tam giác đều, trọng tâm đồng thời là giao điểm của ba đường phân giác. Suy ra, G là tâm đường tròn nội tiếp tam giác ABC.
b) + Gọi D là giao điểm của AG và CB. Khi đó, GD là bán kính đường tròn đường tròn nội tiếp tam giác ABC, AG là bán kính đường tròn ngoại tiếp tam giác ABC.
+ Theo tính chất của trọng tâm trong tam giác ABC ta có: \(GD = \frac{1}{2}AG = \frac{1}{3}AD\).
+ Dựa vào kiến thức bán kính của đường tròn ngoại tiếp bằng \(\frac{\sqrt 3}{3}\) lần độ dài cạnh để tính bán kính đường tròn nội tiếp.
Lời giải chi tiết:
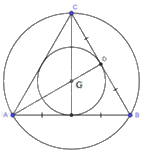
a) Tam giác ABC đều nên G là trọng tâm của tam giác ABC đồng thời là giao điểm của ba đường phân giác. Do đó, G là tâm đường tròn nội tiếp tam giác ABC.
b) Vì G là giao điểm của ba đường trung trực trong tam giác đều ABC (do G là trọng tâm tam giác ABC) nên G là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi D là giao điểm của AG và CB. Suy ra, AG là bán kính đường tròn ngoại tiếp tam giác ABC.
Tam giác ABC đều nên AD là đường trung tuyến đồng thời là đường cao trong tam giác. Do đó, \(GD \bot CB\) tại D. Suy ra, GD là bán kính đường tròn nội tiếp tam giác ABC.
Vì G là trọng tâm tam giác ABC nên \(AG = 2GD\) suy ra \(GD = \frac{1}{2}AG\).
Bán kính đường tròn ngoại tiếp tam giác ABC là: \(AG = \frac{\sqrt 3}{3} BC\)
Do đó, \(GD = \frac{1}{2}.\frac{\sqrt 3}{3} BC = \frac{{\sqrt 3 }}{6}BC\).
Vậy bán kính đường tròn nội tiếp tam giác ABC bằng một nửa đường tròn ngoại tiếp tam giác ABC và bằng \(\frac{{\sqrt 3 }}{6}BC\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 76SGK Toán 9 Kết nối tri thức
Cho tam giác đều ABC (H.9.22).
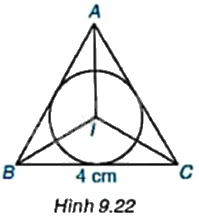
a) Vẽ đường tròn (I; r) nội tiếp tam giác ABC.
b) Biết rằng \(BC = 4cm\), hãy tính bán kính r.
Phương pháp giải:
a) + Vẽ ba đường phân giác của tam giác ABC.
+ Gọi I là giao điểm của ba đường phân giác đó.
+ Gọi H là giao điểm của AI và BC. Vẽ đường tròn tâm I, bán kính IH.
+ Khi đó, đường tròn (I; IH) là đường tròn nội tiếp tam giác ABC cần vẽ.
b) Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\)
Lời giải chi tiết:
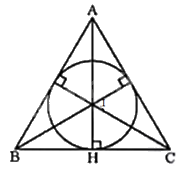
a) Vẽ ba đường phân giác của tam giác ABC. Gọi I là giao điểm của ba đường phân giác đó.
Gọi H là giao điểm của AI và BC. Vẽ đường tròn tâm I, bán kính IH.
Khi đó, đường tròn (I; IH) là đường tròn nội tiếp tam giác ABC cần vẽ.
b) Vì (I; r) nội tiếp tam giác ABC nên bán kính đường tròn nội tiếp tam giác ABC là:
\(r = \frac{{BC\sqrt 3 }}{6} = \frac{{4\sqrt 3 }}{6} = \frac{{2\sqrt 3 }}{3}\left( {cm} \right)\)
Mục 2 của chương trình Toán 9 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc hai. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này yêu cầu học sinh nhắc lại các kiến thức cơ bản về hàm số bậc hai, bao gồm:
Bài tập này tập trung vào việc giải các phương trình bậc hai bằng các phương pháp khác nhau, bao gồm:
Học sinh cần nắm vững các bước giải phương trình bậc hai và lựa chọn phương pháp phù hợp để giải quyết từng bài toán cụ thể.
Bài tập này yêu cầu học sinh vận dụng kiến thức về phương trình bậc hai để giải quyết các bài toán thực tế, ví dụ như:
Việc giải các bài toán thực tế giúp học sinh hiểu rõ hơn về ứng dụng của phương trình bậc hai trong cuộc sống.
Giaitoan.edu.vn cung cấp lời giải chi tiết cho từng bài tập trong mục 2 trang 74, 75, 76 SGK Toán 9 tập 2 - Kết nối tri thức. Các lời giải được trình bày một cách rõ ràng, dễ hiểu, kèm theo các bước giải thích chi tiết và các lưu ý quan trọng.
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 9:
Hy vọng rằng với những hướng dẫn chi tiết và lời giải chính xác của giaitoan.edu.vn, các em học sinh sẽ tự tin hơn trong việc giải các bài tập Toán 9 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!