Giải bài tập 9.6 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức

Bài tập 9.6 trang 71 SGK Toán 9 tập 2 thuộc chương trình Kết nối tri thức là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng về hàm số bậc nhất và ứng dụng của nó. Bài toán này thường yêu cầu học sinh xác định hệ số góc, vẽ đồ thị hàm số và giải các bài toán liên quan đến tính chất của hàm số.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 9.6 trang 71 SGK Toán 9 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Trên sân bóng, khi trái bóng được đặt tại điểm phạt đền thì có góc sút bằng ({36^o}) và trái bóng cách mỗi cọc gôn 11,6m (H.9.11). Hỏi khi trái bóng đặt ở vị trí cách điểm phạt đền 11,6m thì góc sút bằng bao nhiêu?

Đề bài

Trên sân bóng, khi trái bóng được đặt tại điểm phạt đền thì có góc sút bằng \({36^o}\) và trái bóng cách mỗi cọc gôn 11,6m (H.9.11). Hỏi khi trái bóng đặt ở vị trí cách điểm phạt đền 11,6m thì góc sút bằng bao nhiêu?

Giải bài tập 9.6 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức 1

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 9.6 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức 2

+ Chứng minh rằng các cọc gôn, vị trí đặt bóng đều thuộc đường tròn có tâm là điểm phạt đền.

+ Sử dụng liên hệ giữa góc ở tâm và góc nội tiếp cùng chắn một cung trong một đường tròn để tính góc sút phạt.

Lời giải chi tiết

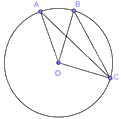
Giải bài tập 9.6 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức 3

Gọi A, B lần lượt là các cọc gôn, C là vị trí đặt bóng, O là chấm phạt đền.

Theo đề bài ta có: \(OA = OB = OC = 11,6m\) nên A, B, C thuộc đường tròn tâm O.

Vì góc nội tiếp ACB và góc ở tâm AOB cùng chắn cung nhỏ AB của đường tròn (O) nên \(\widehat {ACB} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}{.36^o} = {18^o}\)

Vậy khi trái bóng cách vị trí phạt đền 11,6m thì góc sút bằng \({18^o}\).

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 9.6 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức đặc sắc thuộc chuyên mục sách bài tập toán 9 trên nền tảng toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 9.6 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức: Hướng dẫn chi tiết

Bài tập 9.6 trang 71 SGK Toán 9 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc nhất. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:

Hàm số bậc nhất: Dạng y = ax + b, trong đó a là hệ số góc, b là tung độ gốc.
Đồ thị hàm số bậc nhất: Là một đường thẳng.
Tính chất của hàm số bậc nhất: Hàm số đồng biến khi a > 0, nghịch biến khi a < 0.

Đề bài: (Giả sử đề bài là một bài toán cụ thể về quãng đường và vận tốc, ví dụ: Một ô tô đi từ A đến B với vận tốc 60km/h. Hãy viết công thức tính quãng đường đi được sau thời gian t giờ.)

Lời giải:

Xác định hàm số: Gọi s là quãng đường đi được (km), t là thời gian đi (giờ). Ta có hàm số s = 60t.
Phân tích hàm số: Hàm số s = 60t là hàm số bậc nhất với a = 60 > 0, do đó hàm số đồng biến.
Giải thích ý nghĩa của hệ số góc: Hệ số góc a = 60 cho biết cứ mỗi giờ đi được, quãng đường tăng thêm 60km.
Tính quãng đường khi t = 2 giờ: s = 60 * 2 = 120km.

Các dạng bài tập tương tự và phương pháp giải

Ngoài bài tập 9.6, còn rất nhiều bài tập tương tự liên quan đến hàm số bậc nhất. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:

Xác định hàm số khi biết hai điểm thuộc đồ thị: Thay tọa độ hai điểm vào phương trình y = ax + b để tìm a và b.
Tìm giao điểm của hai đường thẳng: Giải hệ phương trình hai đường thẳng để tìm tọa độ giao điểm.
Bài toán ứng dụng: Chuyển bài toán thực tế thành bài toán toán học, sử dụng hàm số bậc nhất để giải quyết.

Lưu ý khi giải bài tập về hàm số bậc nhất

Để giải bài tập về hàm số bậc nhất một cách hiệu quả, các em học sinh cần lưu ý những điều sau:

Nắm vững định nghĩa, tính chất của hàm số bậc nhất.
Biết cách vẽ đồ thị hàm số bậc nhất.
Rèn luyện kỹ năng giải các bài toán ứng dụng.
Thực hành giải nhiều bài tập khác nhau để làm quen với các dạng bài.

Tổng kết

Bài tập 9.6 trang 71 SGK Toán 9 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và hướng dẫn giải các dạng bài tập tương tự, các em học sinh sẽ tự tin hơn khi giải các bài tập toán 9.

Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!