Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 75, 76 sách giáo khoa Toán 9 tập 1 chương trình Kết nối tri thức.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp những lời giải chính xác, logic, giúp các em nắm vững kiến thức và tự tin giải quyết các bài tập tương tự.
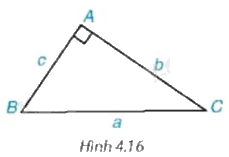
Xét tam giác ABC trong Hình 4.16. a) Viết các tỉ số lượng giác tang, cotang của góc B và góc C theo b và c. b) Tính mỗi cạnh góc vuông b và c theo cạnh góc vuông kia và các tỉ số lượng giác trên của góc B và góc C.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 75SGK Toán 9 Kết nối tri thức
Xét tam giác ABC trong Hình 4.16.
a) Viết các tỉ số lượng giác tang, cotang của góc B và góc C theo b và c.
b) Tính mỗi cạnh góc vuông b và c theo cạnh góc vuông kia và các tỉ số lượng giác trên của góc B và góc C.
Phương pháp giải:
Tỉ số giữa cạnh đối và cạnh kề gọi là tan của góc B, kí hiệu \(\tan \widehat B\)
Tỉ số giữa cạnh kề và cạnh đối gọi là cot của góc B, kí hiệu \(\cot \widehat B\)
Và nếu hai góc phụ nhau (tổng số đo hai góc bằng \({90^0}\)) thì sin góc này bằng cosin góc kia, tan góc này bằng cot góc kia.
Lời giải chi tiết:
a) Tam giác ABC vuông tại A, ta có:
\(\tan \widehat B = \cot \widehat C = \frac{{AC}}{{AB}} = \frac{b}{c}\)
\(\cot \widehat B = \tan \widehat C = \frac{{AB}}{{AC}} = \frac{c}{b}\)
b) Ta có \(\tan \widehat B = \cot \widehat C = \frac{{AC}}{{AB}} = \frac{b}{c}\) nên \(b = c.\tan \widehat B = c.\cot \widehat C\)
Ta có \(\cot \widehat B = \tan \widehat C = \frac{{AB}}{{AC}} = \frac{c}{b}\) nên \(c = b.\cot \widehat B = b.\tan \widehat C\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 76SGK Toán 9 Kết nối tri thức
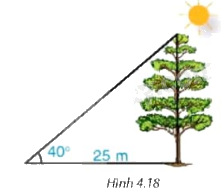
Bóng trên mặt đất của một cây dài 25 m. Tính chiều cao của cây (làm tròn đến dm) , biết rằng tia nắng mặt trời tạo với mặt đất góc \({40^0}\) (H.4.18).
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối hoặc cot góc kề.
Lời giải chi tiết:
Ta có: 25m = 250dm
Chiều cao của cây là \(250.\tan {40^0} \approx 210\) (dm).
Vậy chiều cao của cây khoảng 210dm.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 75SGK Toán 9 Kết nối tri thức
Xét tam giác ABC trong Hình 4.16.
a) Viết các tỉ số lượng giác tang, cotang của góc B và góc C theo b và c.
b) Tính mỗi cạnh góc vuông b và c theo cạnh góc vuông kia và các tỉ số lượng giác trên của góc B và góc C.

Phương pháp giải:
Tỉ số giữa cạnh đối và cạnh kề gọi là tan của góc B, kí hiệu \(\tan \widehat B\)
Tỉ số giữa cạnh kề và cạnh đối gọi là cot của góc B, kí hiệu \(\cot \widehat B\)
Và nếu hai góc phụ nhau (tổng số đo hai góc bằng \({90^0}\)) thì sin góc này bằng cosin góc kia, tan góc này bằng cot góc kia.
Lời giải chi tiết:
a) Tam giác ABC vuông tại A, ta có:
\(\tan \widehat B = \cot \widehat C = \frac{{AC}}{{AB}} = \frac{b}{c}\)
\(\cot \widehat B = \tan \widehat C = \frac{{AB}}{{AC}} = \frac{c}{b}\)
b) Ta có \(\tan \widehat B = \cot \widehat C = \frac{{AC}}{{AB}} = \frac{b}{c}\) nên \(b = c.\tan \widehat B = c.\cot \widehat C\)
Ta có \(\cot \widehat B = \tan \widehat C = \frac{{AB}}{{AC}} = \frac{c}{b}\) nên \(c = b.\cot \widehat B = b.\tan \widehat C\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 76SGK Toán 9 Kết nối tri thức
Bóng trên mặt đất của một cây dài 25 m. Tính chiều cao của cây (làm tròn đến dm) , biết rằng tia nắng mặt trời tạo với mặt đất góc \({40^0}\) (H.4.18).
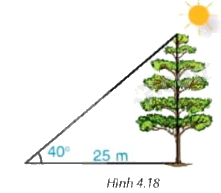
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối hoặc cot góc kề.
Lời giải chi tiết:
Ta có: 25m = 250dm
Chiều cao của cây là \(250.\tan {40^0} \approx 210\) (dm).
Vậy chiều cao của cây khoảng 210dm.
Mục 2 của chương trình Toán 9 tập 1 Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để xác định hàm số, vẽ đồ thị hàm số, và giải các bài toán liên quan đến ứng dụng của hàm số bậc nhất trong thực tế.
Bài 1 yêu cầu học sinh nhắc lại các khái niệm cơ bản về hàm số bậc nhất, bao gồm định nghĩa, dạng tổng quát, hệ số góc, và giao điểm với các trục tọa độ. Việc nắm vững các khái niệm này là nền tảng để giải quyết các bài tập tiếp theo.
Bài 2 tập trung vào việc xác định hàm số bậc nhất khi biết các thông tin về đồ thị hoặc các điểm thuộc đồ thị. Học sinh cần sử dụng các công thức và phương pháp đã học để tìm ra hệ số góc và tung độ gốc của hàm số.
Bài 3 yêu cầu học sinh vẽ đồ thị của hàm số bậc nhất. Để vẽ đồ thị chính xác, học sinh cần xác định ít nhất hai điểm thuộc đồ thị, sau đó nối chúng lại bằng một đường thẳng.
Bài 4 giới thiệu các ứng dụng của hàm số bậc nhất trong thực tế, chẳng hạn như tính quãng đường đi được của một vật chuyển động đều, tính tiền lương theo sản lượng, hoặc tính giá trị của một hàng hóa theo số lượng.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 2 trang 75, 76 SGK Toán 9 tập 1 - Kết nối tri thức:
Ví dụ: Câu a) Hàm số y = 2x + 1 có phải là hàm số bậc nhất không? Vì sao? (Giải thích: Có, vì nó có dạng y = ax + b, với a = 2 và b = 1)
Ví dụ: Xác định hàm số bậc nhất có đồ thị đi qua hai điểm A(1; 2) và B(2; 4). (Giải thích: Thay tọa độ của hai điểm vào phương trình y = ax + b để tìm a và b)
Ví dụ: Vẽ đồ thị của hàm số y = -x + 3. (Giải thích: Xác định hai điểm thuộc đồ thị, chẳng hạn (0; 3) và (3; 0), sau đó nối chúng lại)
Ví dụ: Một ô tô đi từ A đến B với vận tốc 60km/h. Hãy viết hàm số biểu thị quãng đường đi được của ô tô theo thời gian.
Để hiểu rõ hơn về hàm số bậc nhất, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin giải quyết các bài tập trong mục 2 trang 75, 76 SGK Toán 9 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!