Bài tập 5.19 trang 98 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cập nhật lời giải các bài tập Toán 9 tập 1 mới nhất, đảm bảo tính chính xác và đầy đủ.
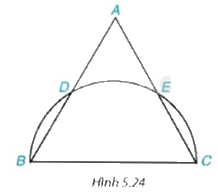
Cho tam giác đều ABC có AB = ({rm{2}}sqrt 3 )cm. Nửa đường tròn đường kính BC cắt hai cạnh AB và AC lần lượt tại D và E (khác B và C) (H.5.24). a) Chứng tỏ rằng ba cung nhỏ BD, DE và EC bằng nhau. Tính số đo mỗi cung ấy. b) Tính diện tích của hình viên phân (xem ví dụ 2) giới hạn bởi dây BD và cung nhỏ BD.
Đề bài
Cho tam giác đều ABC có AB = \({\rm{2}}\sqrt 3 \)cm. Nửa đường tròn đường kính BC cắt hai cạnh AB và AC lần lượt tại D và E (khác B và C) (H.5.24).
a) Chứng tỏ rằng ba cung nhỏ BD, DE và EC bằng nhau. Tính số đo mỗi cung ấy.
b) Tính diện tích của hình viên phân (xem ví dụ 2) giới hạn bởi dây BD và cung nhỏ BD.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng mình tam giác OBD đều, từ đó suy ra \(\widehat {{\rm{BOD}}} = 60^\circ \). Tương tự có: \(\widehat {{\rm{BOD}}} = \widehat {{\rm{COE}}} = \widehat {{\rm{DOE}}} = 60^\circ \) hay số đo các cung nhỏ BD, DE và EC bằng nhau.
b) Áp dụng công thức tính diện tích hình viên phân: \(S = {R^2}\left( {\frac{\pi }{4} - \frac{1}{2}} \right)\)
Lời giải chi tiết
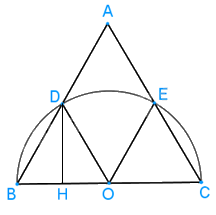
a) Gọi O là trung điểm của BC
Vì OB = OD nên tam giác OBD là tam giác cân tại O
Mà \(\widehat {{\rm{OBD}}} = 60^\circ \)(do tam giác ABC đều)
Suy ra tam giác OBD đều.
Do đó: \(\widehat {{\rm{BOD}}} = 60^\circ \)
Tương tự ta có: \(\widehat {{\rm{COE}}} = 60^\circ \)
Lại có: \(\widehat {{\rm{BOD}}} + \widehat {{\rm{DOE}}} + \widehat {{\rm{COE}}} = 180^\circ \Rightarrow \widehat {{\rm{DOE}}} = 60^\circ \)
Khi đó: \(\widehat {{\rm{BOD}}} = \widehat {{\rm{COE}}} = \widehat {{\rm{DOE}}} = 60^\circ \)
Hay sđ\(\overset\frown{BD}=\) sđ\(\overset\frown{CE}=\) sđ\(\overset\frown{DE}=60{}^\circ \)
b) Đường tròn (O) có bán kính \(OA = \frac{{AB}}{2} = \frac{{{\rm{2}}\sqrt 3 }}{2} = \sqrt 3 \)(cm)
\(S_q = \frac{60}{360}.\pi.(\sqrt{3})^2 = \frac{\pi}{2} (cm^2) \)
Kẻ \(DH \bot OB\), tam giác OBD đều nên DH cũng là đường trung tuyến, suy ra H là trung điểm của OB.
Suy ra \( OH = \frac{OB}{2} = \frac{\sqrt 3}{2}\)
Áp dụng định lí Pythagore vào tam giác ODH, ta có:
\(DH = \sqrt{OD^2-OH^2} = \sqrt{3 - \left({\frac{\sqrt3}{2}}\right)^2} = \frac{3}{2}\)
Diện tích tam giác OBD là:
\(S_{\Delta OBD} = \frac{DH.OB}{2} = \frac{3.\sqrt3}{2.2} = \frac{3\sqrt3}{4}\)
Diện tích hình viên phân là:
\(S_{vp} = S_q - S_{\Delta OBD} = \frac{\pi}{2} - \frac{3\sqrt3}{4} \approx 0,27 (cm^2)\)
Bài tập 5.19 trang 98 SGK Toán 9 tập 1 - Kết nối tri thức là một bài toán ứng dụng thực tế về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Đề bài: (Nội dung đề bài đầy đủ của bài tập 5.19)
Lời giải:
Giải thích chi tiết từng bước:
Bước 1: (Giải thích chi tiết bước 1, ví dụ: Đề bài cho biết... Do đó, ta có thể xác định...)
Bước 2: (Giải thích chi tiết bước 2, ví dụ: Vì hàm số là bậc nhất, ta có thể viết phương trình...)
Bước 3: (Giải thích chi tiết bước 3, ví dụ: Thay các giá trị đã biết vào phương trình, ta được...)
Bước 4: (Giải thích chi tiết bước 4, ví dụ: Kết quả này phù hợp với điều kiện của đề bài...)
Để hiểu rõ hơn về cách giải bài tập 5.19, chúng ta hãy xem xét một ví dụ minh họa sau:
(Nêu một ví dụ tương tự bài tập 5.19 và giải chi tiết)
Để củng cố kiến thức về hàm số bậc nhất, bạn có thể làm thêm các bài tập sau:
Bài tập 5.19 trang 98 SGK Toán 9 tập 1 - Kết nối tri thức là một bài toán quan trọng giúp học sinh hiểu rõ hơn về ứng dụng của hàm số bậc nhất trong thực tế. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.