Bài tập 2.4 trang 30 SGK Toán 9 tập 1 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải phương trình bậc hai. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về công thức nghiệm, định lý Vi-et và các phương pháp giải phương trình khác nhau.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 2.4 trang 30 SGK Toán 9 tập 1 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
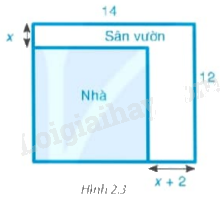
Bác An có một mảnh đất hình chữ nhật với chiều dài 14m và chiều rộng 12m. Bác dự định xây nhà trên mảnh đất đó và dành một phần diện tích đất để làm sân vườn như hình 2.3. Biết diện tích đất làm nhà là (100{m^2}.) Hỏi x bằng bao nhiêu mét?
Đề bài
Bác An có một mảnh đất hình chữ nhật với chiều dài 14m và chiều rộng 12m. Bác dự định xây nhà trên mảnh đất đó và dành một phần diện tích đất để làm sân vườn như hình 2.3. Biết diện tích đất làm nhà là \(100{m^2}.\) Hỏi x bằng bao nhiêu mét?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Ta biểu diễn các cạnh của phần đất làm nhà theo độ dài của mảnh đất.
Viết phương trình biểu diễn diện tích phần đất làm nhà.
Giải phương trình để tìm x.
Lời giải chi tiết
ĐK: \(0<x<12\)
Ta có phần đất làm nhà có kích thước như sau:
- Một cạnh là: \(12 - x\) (m)
- Cạnh còn lại là: \(14 - (x + 2) = 12 - x\) (m)
Vì diện tích đất làm nhà là \(100m^2\) nên ta có phương trình:
\((12 - x).(12 - x) = 100\)
\((12-x)^2-10^2 = 0\)
\((12-x-10)(12-x+10)=0\)
\((2-x)(22-x)=0\)
\(x=2\) (thỏa mãn) hoặc \(x = 22\) (không thỏa mãn)
Vậy \(x = 2m\).
Bài tập 2.4 trang 30 SGK Toán 9 tập 1 - Kết nối tri thức yêu cầu giải các phương trình bậc hai. Để giải quyết bài tập này, chúng ta cần nắm vững các kiến thức cơ bản về phương trình bậc hai, bao gồm:
Bài tập 2.4 thường bao gồm nhiều phương trình bậc hai khác nhau. Để giải quyết hiệu quả, chúng ta nên phân tích từng phương trình một cách cẩn thận. Xác định các hệ số a, b, c của mỗi phương trình. Sau đó, tính biệt thức Δ để xác định số nghiệm của phương trình.
Giả sử phương trình đầu tiên trong bài tập 2.4 là: 2x2 - 5x + 2 = 0
Giả sử phương trình thứ hai trong bài tập 2.4 là: x2 - 4x + 4 = 0
Phương trình bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:
Việc nắm vững kiến thức về phương trình bậc hai và luyện tập thường xuyên là rất quan trọng để đạt kết quả tốt trong môn Toán 9. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết bài tập 2.4 trang 30 SGK Toán 9 tập 1 - Kết nối tri thức một cách hiệu quả.