Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong sách giáo khoa Toán 9 tập 2 - Kết nối tri thức, đặc biệt là mục 1 trang 94, 95, 96.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt trong môn Toán.
Nêu một số đồ vật có dạng hình trụ trong đời sống.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 95SGK Toán 9 Kết nối tri thức
Hãy nhắc lại công thức tính thể tích của hình lăng trụ đứng tam giác (hoặc hình lăng trụ đứng tứ giác) có diện tích đáy S và chiều cao h.
Phương pháp giải:
Nhớ lại công thức tính thể tích hình lăng trụ đứng tam giác (tứ giác) đã học ở lớp 7.
Lời giải chi tiết:
Thể tích của hình lăng trụ đứng tam giác (hoặc hình lăng trụ đứng tứ giác) có diện tích đáy S và chiều cao h là: \(V = S.h\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 95SGK Toán 9 Kết nối tri thức
Người ta coi diện tích hình chữ nhật ABCD chính là diện tích xung quanh của hình trụ được tạo thành (xem Thực hành 1). Cho hình trụ có chiều cao \(h = 9cm\) và bán kính đáy \(R = 5cm\). Tính diện tích mặt xung quanh của hình trụ.
Phương pháp giải:
Hình chữ nhật ABCD có một cạnh bằng chu vi hình tròn đáy, cạnh còn lại bằng chiều cao của hình trụ.
Lời giải chi tiết:
Hình chữ nhật ABCD có một cạnh bằng chu vi hình tròn đáy, cạnh còn lại bằng chiều cao của hình trụ.
Nên ta có một cạnh của hình chữ nhật bằng 9cm.
Cạnh còn lại của hình chữ nhật (hay chu vi hình tròn đáy) là:
\(2.\pi .R = 2.\pi .5 = 10\pi \)
Diện tích hình chữ nhật ABCD là: \(10\pi .9 = 90\pi \left( {c{m^2}} \right)\).
Do đó, diện tích xung quanh của hình trụ là \(90\pi c{m^2}\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 96 SGK Toán 9 Kết nối tri thức
Một thùng nước có dạng hình trụ với chiều cao bằng 1,6m và bán kính đáy bằng 0,5m.
a) Tính diện tích xung quanh của thùng nước.
b) Hỏi thùng nước chứa được bao nhiêu lít nước?
(Coi chiều dày của thùng không đáng kể và làm tròn kết quả ở câu b đến hàng đơn vị của lít).
Phương pháp giải:
a) Diện tích xung quanh của hình trụ có bán kính đáy R và chiều cao h là: \({S_{xq}} = 2\pi Rh\).
b) Thể tích của hình trụ có bán kính đáy R và chiều cao h là: V = Sđáy.h\( = \pi {R^2}h\).
Lời giải chi tiết:
a) Diện tích xung quanh của thùng nước là: \({S_{xq}} = 2.\pi .0,5.1,6 = 1,6\pi \left( {{m^2}} \right)\).
b) Thể tích của thùng nước là: \(V = \pi .0,{5^2}.1,6 = 0,4\pi \approx 1,257\left( {{m^3}} \right)\)
Đổi \(1,257{m^3} = 1\;257\left( l \right)\)
Vậy thùng nước chứa được khoảng 1 257 lít nước.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 95SGK Toán 9 Kết nối tri thức
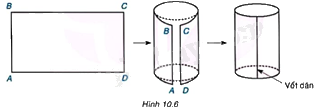
Chuẩn bị một băng giấy cứng hình chữ nhật ABCD với \(AB = 8cm,BC = 15cm\). Cuộn băng giấy lại sao cho hai cạnh AB và DC sát vào nhau như Hình 10.6 (dùng băng keo dán), ta được một hình trụ (không có đáy). Hãy cho biết chiều cao và chu vi đáy của hình trụ đó.
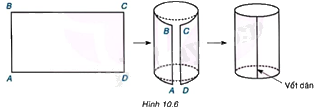
Phương pháp giải:
Chiều cao của hình trụ chính là đoạn thẳng AB.
Chu vi hình tròn chính là độ dài đoạn thẳng BC.
Lời giải chi tiết:
Chiều cao của hình trụ đó chính là đoạn thẳng AB nên chiều cao bằng 8cm.
Vì băng giấy được cuộn vào nên ta được hai đáy tạo thành các hình tròn, nên chu vi hình tròn là đoạn thẳng BC. Do đó chu vi đáy của hình trụ bằng \(15cm\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 94 SGK Toán 9 Kết nối tri thức
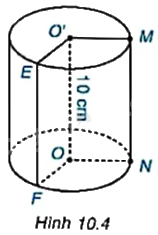
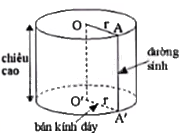
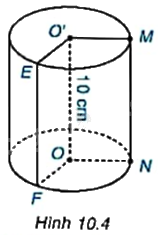
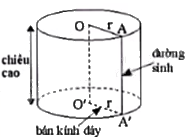
Kể tên các bán kính đáy và đường sinh còn lại của hình trụ có trong Hình 10.4.
Phương pháp giải:
Dựa vào đặc điểm của hình trụ:
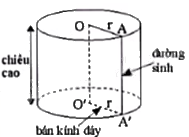
Lời giải chi tiết:
ON, OF, O’E là các bán kính đáy của hình trụ.
MN là đường sinh của hình trụ.
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 94SGK Toán 9 Kết nối tri thức
Nêu một số đồ vật có dạng hình trụ trong đời sống.
Phương pháp giải:
Hình trụ có dạng:
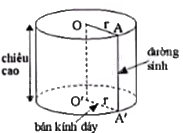
Lời giải chi tiết:
Một số đồ vật có dạng hình trụ trong cuộc sống:

Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 94SGK Toán 9 Kết nối tri thức
Nêu một số đồ vật có dạng hình trụ trong đời sống.
Phương pháp giải:
Hình trụ có dạng:
Lời giải chi tiết:
Một số đồ vật có dạng hình trụ trong cuộc sống:

Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 94 SGK Toán 9 Kết nối tri thức
Kể tên các bán kính đáy và đường sinh còn lại của hình trụ có trong Hình 10.4.
Phương pháp giải:
Dựa vào đặc điểm của hình trụ:
Lời giải chi tiết:
ON, OF, O’E là các bán kính đáy của hình trụ.
MN là đường sinh của hình trụ.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 95SGK Toán 9 Kết nối tri thức
Chuẩn bị một băng giấy cứng hình chữ nhật ABCD với \(AB = 8cm,BC = 15cm\). Cuộn băng giấy lại sao cho hai cạnh AB và DC sát vào nhau như Hình 10.6 (dùng băng keo dán), ta được một hình trụ (không có đáy). Hãy cho biết chiều cao và chu vi đáy của hình trụ đó.
Phương pháp giải:
Chiều cao của hình trụ chính là đoạn thẳng AB.
Chu vi hình tròn chính là độ dài đoạn thẳng BC.
Lời giải chi tiết:
Chiều cao của hình trụ đó chính là đoạn thẳng AB nên chiều cao bằng 8cm.
Vì băng giấy được cuộn vào nên ta được hai đáy tạo thành các hình tròn, nên chu vi hình tròn là đoạn thẳng BC. Do đó chu vi đáy của hình trụ bằng \(15cm\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 95SGK Toán 9 Kết nối tri thức
Người ta coi diện tích hình chữ nhật ABCD chính là diện tích xung quanh của hình trụ được tạo thành (xem Thực hành 1). Cho hình trụ có chiều cao \(h = 9cm\) và bán kính đáy \(R = 5cm\). Tính diện tích mặt xung quanh của hình trụ.
Phương pháp giải:
Hình chữ nhật ABCD có một cạnh bằng chu vi hình tròn đáy, cạnh còn lại bằng chiều cao của hình trụ.
Lời giải chi tiết:
Hình chữ nhật ABCD có một cạnh bằng chu vi hình tròn đáy, cạnh còn lại bằng chiều cao của hình trụ.
Nên ta có một cạnh của hình chữ nhật bằng 9cm.
Cạnh còn lại của hình chữ nhật (hay chu vi hình tròn đáy) là:
\(2.\pi .R = 2.\pi .5 = 10\pi \)
Diện tích hình chữ nhật ABCD là: \(10\pi .9 = 90\pi \left( {c{m^2}} \right)\).
Do đó, diện tích xung quanh của hình trụ là \(90\pi c{m^2}\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 95SGK Toán 9 Kết nối tri thức
Hãy nhắc lại công thức tính thể tích của hình lăng trụ đứng tam giác (hoặc hình lăng trụ đứng tứ giác) có diện tích đáy S và chiều cao h.
Phương pháp giải:
Nhớ lại công thức tính thể tích hình lăng trụ đứng tam giác (tứ giác) đã học ở lớp 7.
Lời giải chi tiết:
Thể tích của hình lăng trụ đứng tam giác (hoặc hình lăng trụ đứng tứ giác) có diện tích đáy S và chiều cao h là: \(V = S.h\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 96 SGK Toán 9 Kết nối tri thức
Một thùng nước có dạng hình trụ với chiều cao bằng 1,6m và bán kính đáy bằng 0,5m.
a) Tính diện tích xung quanh của thùng nước.
b) Hỏi thùng nước chứa được bao nhiêu lít nước?
(Coi chiều dày của thùng không đáng kể và làm tròn kết quả ở câu b đến hàng đơn vị của lít).
Phương pháp giải:
a) Diện tích xung quanh của hình trụ có bán kính đáy R và chiều cao h là: \({S_{xq}} = 2\pi Rh\).
b) Thể tích của hình trụ có bán kính đáy R và chiều cao h là: V = Sđáy.h\( = \pi {R^2}h\).
Lời giải chi tiết:
a) Diện tích xung quanh của thùng nước là: \({S_{xq}} = 2.\pi .0,5.1,6 = 1,6\pi \left( {{m^2}} \right)\).
b) Thể tích của thùng nước là: \(V = \pi .0,{5^2}.1,6 = 0,4\pi \approx 1,257\left( {{m^3}} \right)\)
Đổi \(1,257{m^3} = 1\;257\left( l \right)\)
Vậy thùng nước chứa được khoảng 1 257 lít nước.
Mục 1 của chương trình Toán 9 tập 2 - Kết nối tri thức thường tập trung vào các chủ đề quan trọng như hàm số bậc hai, đồ thị hàm số bậc hai, phương trình bậc hai và ứng dụng của chúng. Việc nắm vững kiến thức trong mục này là nền tảng để giải quyết các bài toán phức tạp hơn trong các chương tiếp theo.
Các bài tập trên trang 94 thường yêu cầu học sinh xác định hệ số a, b, c của hàm số bậc hai, tìm đỉnh của parabol, vẽ đồ thị hàm số và xác định khoảng đồng biến, nghịch biến của hàm số. Để giải các bài tập này, học sinh cần nắm vững định nghĩa hàm số bậc hai, công thức tính đỉnh của parabol và các tính chất của đồ thị hàm số bậc hai.
Trang 95 tập trung vào việc giải các phương trình bậc hai bằng các phương pháp khác nhau như phân tích thành nhân tử, sử dụng công thức nghiệm và phương pháp hoàn thiện bình phương. Học sinh cần thành thạo các phương pháp này để có thể giải quyết mọi loại phương trình bậc hai.
Các bài tập trên trang 96 thường yêu cầu học sinh vận dụng kiến thức về phương trình bậc hai để giải quyết các bài toán thực tế như bài toán về chuyển động, bài toán về diện tích, bài toán về năng suất lao động. Đây là cơ hội để học sinh rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Giaitoan.edu.vn cung cấp lời giải chi tiết cho từng bài tập trong mục 1 trang 94, 95, 96 SGK Toán 9 tập 2 - Kết nối tri thức. Các lời giải được trình bày một cách rõ ràng, dễ hiểu, kèm theo các bước giải cụ thể và các lưu ý quan trọng. Học sinh có thể tham khảo các lời giải này để hiểu rõ hơn về cách giải bài tập và tự mình giải các bài tập tương tự.
Ví dụ 1: Giải phương trình 2x2 - 5x + 2 = 0
Ví dụ 2: Tìm đỉnh của parabol y = x2 - 4x + 3
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 94, 95, 96 SGK Toán 9 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!