Bài tập 6.14 trang 17 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 6.14 trang 17 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
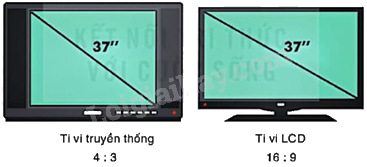
Kích thước màn hình ti vi hình chữ nhật được xác định bằng độ dài đường chéo. Ti vi truyền thống có định dạng 4:3, nghĩa là tỉ lệ giữa chiều dài và chiều rộng của màn hình là 4:3. Hỏi diện tích của màn hình ti vi truyền thống 37in là bao nhiêu? Diện tích của màn hình ti vi LCD 37 in có định dạng 16:9 là bao nhiêu? Màn hình ti vi nào có diện tích lớn hơn? Ở đây, các diện tích màn hình được tính bằng inch vuông.
Đề bài
Kích thước màn hình ti vi hình chữ nhật được xác định bằng độ dài đường chéo. Ti vi truyền thống có định dạng 4:3, nghĩa là tỉ lệ giữa chiều dài và chiều rộng của màn hình là 4:3. Hỏi diện tích của màn hình ti vi truyền thống 37in là bao nhiêu? Diện tích của màn hình ti vi LCD 37 in có định dạng 16:9 là bao nhiêu? Màn hình ti vi nào có diện tích lớn hơn? Ở đây, các diện tích màn hình được tính bằng inch vuông.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Gọi chiều dài của ti vi là x, đặt điều kiện, tính chiều rộng theo x.
+ Áp dụng định lý Pythagore để đưa ra phương trình theo ẩn x.
+ Giải phương trình ẩn x, tìm nghiệm x, đối chiếu với điều kiện để tìm giá trị x thỏa mãn điều kiện.
+ Tính diện tích của ti vi.
+ So sánh diện tích của ti vi truyền thống và ti vi LCD và đưa ra kết luận.
Lời giải chi tiết
+) Gọi chiều dài của ti vi truyền thống là x (in, \(x > 0\)) thì chiều rộng của ti vi truyền thống là \(\frac{3}{4}x\left( {in} \right)\)
Khi đó ta có: \({x^2} + {\left( {\frac{3}{4}x} \right)^2} = {37^2}\) (định lý Pythagore)
\(\frac{{25}}{{16}}{x^2} = 1369\)
\(x = \frac{{148}}{5}\) (do \(x > 0\))
Diện tích của ti vi truyền thống là: \(\frac{{148}}{5}.\frac{3}{4}.\frac{{148}}{5} = 657,12\left( {i{n^2}} \right)\)
+) Gọi chiều dài của ti vi LCD là y (in, \(y > 0\)) thì chiều rộng của ti vi LCD là \(\frac{9}{{16}}y\left( {in} \right)\)
Khi đó ta có: \({y^2} + {\left( {\frac{9}{{16}}y} \right)^2} = {37^2}\) (định lý Pythagore)
\(\frac{{337}}{{256}}{y^2} = 1369\)
\({y^2} = \frac{{350464}}{{337}}\)
Diện tích của ti vi LCD là:
\(\frac{9}{{16}}{y^2} = \frac{9}{{16}}.\frac{{350464}}{{337}} \approx 584,97 \left( {i{n^2}} \right)\)
Vì \(584,97 < 657,12\) nên màn hình ti vi truyền thống có diện tích lớn hơn.
Bài tập 6.14 SGK Toán 9 tập 2 Kết nối tri thức là một bài toán thực tế, yêu cầu học sinh xây dựng và giải hệ phương trình bậc nhất hai ẩn. Để giải bài tập này, các em cần nắm vững các kiến thức sau:
Bài toán 6.14 SGK Toán 9 tập 2 thường mô tả một tình huống thực tế, trong đó có hai đại lượng liên quan đến nhau. Nhiệm vụ của học sinh là xác định hai đại lượng đó, đặt ẩn số và xây dựng hệ phương trình bậc nhất hai ẩn để mô tả mối quan hệ giữa chúng. Sau đó, giải hệ phương trình để tìm ra giá trị của các ẩn số, từ đó giải quyết bài toán.
(Ở đây sẽ là lời giải chi tiết của bài tập 6.14, bao gồm các bước giải, giải thích rõ ràng và kết luận. Ví dụ:)
Ví dụ: Giả sử bài toán yêu cầu tìm chiều dài và chiều rộng của một mảnh đất hình chữ nhật, biết chu vi của mảnh đất là 50m và chiều dài hơn chiều rộng 5m.
Để củng cố kiến thức về hệ phương trình bậc nhất hai ẩn và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập sau:
Khi giải các bài toán về hệ phương trình bậc nhất hai ẩn, các em cần chú ý:
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ tự tin giải bài tập 6.14 trang 17 SGK Toán 9 tập 2 - Kết nối tri thức và đạt kết quả tốt trong môn Toán.