Bài tập 8.11 trang 65 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 8.11 trang 65 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Trên một dãy phố có ba quán ăn A, B, C. Hai bạn Văn và Hải mỗi người chọn ngẫu nhiên một quán ăn để ăn trưa. a) Mô tả không gian mẫu của phép thử. b) Tính xác suất của các biến cố sau: E: “Hai bạn cùng vào một quán”; F: “Cả hai bạn không chọn quán C”; G: “Có ít nhất một bạn chọn quán B”.
Đề bài
Trên một dãy phố có ba quán ăn A, B, C. Hai bạn Văn và Hải mỗi người chọn ngẫu nhiên một quán ăn để ăn trưa.
a) Mô tả không gian mẫu của phép thử.
b) Tính xác suất của các biến cố sau:
E: “Hai bạn cùng vào một quán”;
F: “Cả hai bạn không chọn quán C”;
G: “Có ít nhất một bạn chọn quán B”.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về không gian mẫu để tìm không gian mẫu: Tập hợp tất cả các kết quả có thể xảy ra của phép thử (gọi tắt là tập tất cả các kết quả có thể của phép thử) được gọi là không gian mẫu của phép thử.
Ta có thể tìm số phần tử của không gian mẫu bằng cách lập bảng.
b) Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết
a) Ta liệt kê tất cả các kết quả có thể của phép thử bằng cách lập bảng:
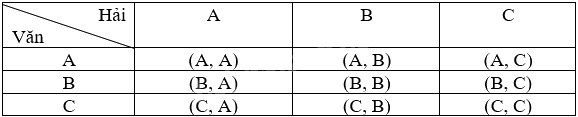
Không gian mẫu của phép thử là: \(\Omega = \){(A, A), (B, A), (C, A), (A, B), (B, B), (C, B), (A, C), (B, C), (C, C)}. Vậy không gian mẫu có 9 phần tử.
b) Vì hai bạn Văn và Hải mỗi người chọn ngẫu nhiên một quán ăn để ăn trưa nên các kết quả có thể của phép thử là đồng khả năng.
Có 3 kết quả thuận lợi của biến cố E là: (A, A), (B, B), (C, C). Do đó, \(P\left( E \right) = \frac{3}{9} = \frac{1}{3}\).
Có 4 kết quả thuận lợi của biến cố F là: (A, A), (B, B), (A, B), (B, A). Do đó, \(P\left( F \right) = \frac{4}{9}\).
Có 5 kết quả thuận lợi của biến cố G là: (C, B), (B, B), (A, B), (B, A), (B, C). Do đó, \(P\left( G \right) = \frac{5}{9}\).
Bài tập 8.11 trang 65 SGK Toán 9 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc nhất và hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Trước khi đi vào giải bài tập, chúng ta cần phân tích kỹ đề bài để xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Thông thường, bài toán sẽ cung cấp các thông tin về một tình huống thực tế, chẳng hạn như quãng đường đi được của một vật, giá trị của một sản phẩm, hoặc số lượng sản phẩm bán được. Dựa vào các thông tin này, chúng ta cần xây dựng được một mô hình toán học phù hợp, thường là một hàm số bậc nhất hoặc hàm số bậc hai.
(Nội dung lời giải chi tiết bài tập 8.11 sẽ được trình bày tại đây, bao gồm các bước giải, các công thức sử dụng, và các giải thích rõ ràng để học sinh dễ hiểu. Ví dụ:)
Ví dụ: Giả sử bài toán yêu cầu tìm phương trình đường thẳng đi qua hai điểm A(1; 2) và B(3; 4). Chúng ta có thể giải bài toán này như sau:
Ngoài bài tập 8.11, còn rất nhiều bài tập tương tự trong chương trình Toán 9 Kết nối tri thức. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập về hàm số một cách hiệu quả, các em học sinh có thể tham khảo một số mẹo sau:
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số, các em học sinh nên luyện tập thêm các bài tập khác trong SGK và các tài liệu tham khảo. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng, giúp các em học sinh rèn luyện và nâng cao khả năng giải toán.
Bài tập 8.11 trang 65 SGK Toán 9 tập 2 là một bài tập quan trọng trong chương trình Toán 9 Kết nối tri thức. Việc nắm vững phương pháp giải bài tập này sẽ giúp các em học sinh tự tin giải các bài tập tương tự và đạt kết quả tốt trong các kỳ thi và kiểm tra. Hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về bài tập này và có thể tự giải quyết các bài toán tương tự một cách hiệu quả.