Chào mừng bạn đến với bài học về Lý thuyết Đa giác đều trong chương trình Toán 9 Kết nối tri thức tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về đa giác đều, giúp bạn tự tin giải quyết các bài tập liên quan.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất, công thức tính toán và các ứng dụng thực tế của đa giác đều. Hãy cùng bắt đầu!
1. Đa giác đều Đa giác Những hình như dưới đây được gọi chung là các đa giác.
1. Đa giác đều
Đa giác
Những hình như dưới đây được gọi chung là các đa giác.
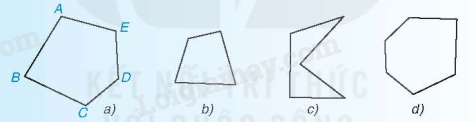
- Đa giác ABCDE (hình a) là hình gồm năm đoạn thẳng AB, BC, CD, DE, EA, trong đó bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng.
Đa giác ABCDE có:
+ năm đỉnh là các điểm A, B, C, D, E,
+ năm cạnh là các đoạn thẳng AB, BC, CD, DE, EA
+ năm góc là các góc EAB, ABC, BCD, CDE, DEA.
- Nếu với một cạnh bất kì, các đỉnh không thuộc cạnh đó đều nằm về một phía đối với đường thẳng chứa cạnh đó thì đa giác được gọi là đa giác lồi. Các đa giác trong a, b, d là các đa giác lồi. Đa giác trong c không phải đa giác lồi.
Đa giác đều
Đa giác đều là một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau. |
Các đỉnh của mỗi đa giác đều luôn cùng nằm trên một đường tròn, được gọi là đường tròn ngoại tiếp đa giác, tâm đường tròn được gọi là tâm của đa giác và đa giác được gọi là nội tiếp đường tròn đó.
Ví dụ: Một số hình đa giác đều thường gặp trong hình học:

2. Phép quay
Khái niệm phép quay
Phép quay thuận chiều \(\alpha ^\circ \) (0° < \(\alpha ^\circ \) < 360°) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \(\alpha ^\circ \) (hình a). Định nghĩa tương tự cho phép quay ngược chiều \(\alpha ^\circ \) tâm O (hình b). Chú ý: Phép quay 0° và phép quay 360° giữ nguyên mọi điểm.
|
Phép quay giữ nguyên hình đa giác đều
Một phép quay được gọi là giữ nguyên một đa giác đều ℋ nếu phép quay đó biến mỗi điểm của ℋ thành một điểm của ℋ. Nếu một phép quay biến các đỉnh của đa giác đều ℋ thành các đỉnh của ℋ thì phép quay đó giữ nguyên ℋ. |
Ví dụ:
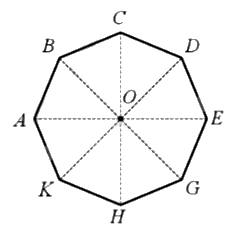
Phép quay thuận chiều \(45^\circ \) tâm O biến điểm A thành điểm B thì phép quay đó biến các điểm C, D, H, K tương ứng thành các điểm D, E, K, A.
Đa giác đều là một khái niệm quan trọng trong hình học, đặc biệt trong chương trình Toán 9 Kết nối tri thức. Hiểu rõ về đa giác đều không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng cho việc học các môn học liên quan sau này.
Một đa giác được gọi là đa giác đều nếu nó vừa là đa giác lồi vừa có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau. Nói cách khác, một đa giác đều là một đa giác có tính đối xứng cao.
Có một số công thức quan trọng liên quan đến đa giác đều:
Đa giác đều có một số tính chất quan trọng:
Bài 1: Tính số đo mỗi góc trong của một lục giác đều.
Giải: Số đo mỗi góc trong của một lục giác đều là [(6 - 2) * 180°] / 6 = 120°
Bài 2: Một ngũ giác đều có cạnh dài 5cm. Tính diện tích của ngũ giác đều đó.
Giải: Diện tích của ngũ giác đều là (5 * 52) / (4 * tan(π/5)) ≈ 43.01 cm2
Đa giác đều xuất hiện rất nhiều trong thực tế:
Để nắm vững kiến thức về đa giác đều, bạn nên luyện tập thêm các bài tập khác nhau. Bạn có thể tìm thấy các bài tập này trong sách giáo khoa, các trang web học toán online hoặc các tài liệu tham khảo khác.
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về Lý thuyết Đa giác đều Toán 9 Kết nối tri thức. Chúc bạn học tập tốt!