Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK Toán 9 tập 2, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 2 trang 39, 40, 41 của sách Toán 9 tập 2 - Kết nối tri thức. Các em hãy chuẩn bị sách giáo khoa và cùng chúng tôi bắt đầu nhé!
Có ba phương án thi đấu tại giải bóng đá khối lớp 9 của một trường như sau: Phương án 1: Các đội đấu vòng tròn, tính điểm; Phương án 2: Chia các đội thành hai bảng, mỗi bảng lấy hai đội vào trận bán kết; Phương án 3: Các đội bốc thăm ghép cặp, đấu loại trực tiếp. Ban tổ chức đã lấy phiếu khảo sát ý kiến. Kết quả được Bình và Nam biểu diễn bằng các biểu đồ như sau: a) Đọc và giải thích mỗi biểu đồ trên. b) Lập bảng tần số tương đối cho kết quả khảo sát ý kiến trên.
Video hướng dẫn giải
Trả lời câu hỏi Tranh luận trang 41 SGK Toán 9 Kết nối tri thức
Bạn Bình phát phiếu (H.7.13) lấy ý kiến bình chọn của 40 bạn trong lớp về địa điểm đi dã ngoại. Kết quả bạn Bình thu được như sau:


Vuông: Tớ sẽ dùng biểu đồ hình quạt tròn để biểu diễn bảng thống kê này.
Tròn: Không được. Cậu phải dùng biểu đồ cột để biểu diễn.
Ý kiến của bạn thế nào?
Phương pháp giải:
Sử dụng kiến thức về biểu đồ hình quạt tròn để giải thích.
Lời giải chi tiết:
Vì tổng số phần trăm tỉ lệ bình chọn của ba vườn quốc gia lớn hơn 100% nên không dùng biểu đồ hình quạt tròn để thể hiện bảng thống kê này được.
Có thể dùng biểu đồ cột để biểu diễn.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 41 SGK Toán 9 Kết nối tri thức
Bảng tần số tương đối sau cho biết tỉ lệ học sinh đánh giá độ khó của đề thi học kì môn Toán theo các mức độ.

Vẽ biểu đồ hình quạt tròn biểu diễn bảng tần số tương đối này.
Phương pháp giải:
Cách vẽ biểu đồ tần số tương đối:
Bước 1: Xác định số đo cung tương ứng của các hình quạt dùng để biểu diễn tần số tương đối của các giá trị theo công thức \({360^o}.{f_i}\) với \(i = 1,...,k\).
Bước 2: Vẽ hình tròn và chia hình tròn thành các hình quạt có số đo cung tương ứng được xác định trong Bước 1.
Bước 3: Định dạng các hình quạt tròn (thường bằng cách tô màu), ghi tần số tương đối, chú giải và tiêu đề.
Lời giải chi tiết:
Bước 1: Xác định số đo cung tương ứng của các hình quạt biểu diễn các tần số tương đối cho độ khó môn Toán:
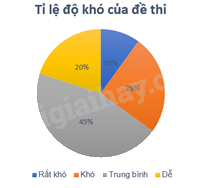
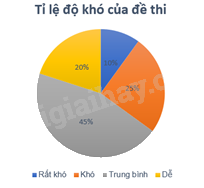
Rất khó: \({360^o}.10\% = {36^o}\), khó: \({360^o}.25\% = {90^o}\), trung bình: \({360^o}.45\% = {162^o}\), dễ: \({360^o}.20\% = {72^o}\).
Bước 2: Vẽ hình tròn và chia hình tròn thành các hình quạt:
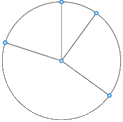
Bước 3: Định dạng các hình quạt tròn, ghi tỉ lệ phần trăm, chú giải và tiêu đề.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 39 SGK Toán 9 Kết nối tri thức
Có ba phương án thi đấu tại giải bóng đá khối lớp 9 của một trường như sau:
Phương án 1: Các đội đấu vòng tròn, tính điểm;
Phương án 2: Chia các đội thành hai bảng, mỗi bảng lấy hai đội vào trận bán kết;
Phương án 3: Các đội bốc thăm ghép cặp, đấu loại trực tiếp.
Ban tổ chức đã lấy phiếu khảo sát ý kiến. Kết quả được Bình và Nam biểu diễn bằng các biểu đồ như sau:
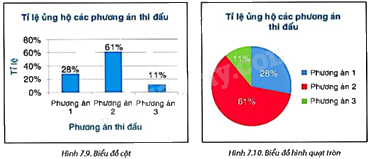
a) Đọc và giải thích mỗi biểu đồ trên.
b) Lập bảng tần số tương đối cho kết quả khảo sát ý kiến trên.
Phương pháp giải:
a) Chỉ ra tỉ lệ ủng hộ cho các phương án 1; 2; 3.
b) + Dựa vào biểu đồ chỉ ra tần số tương đối ứng với các giá trị trong mẫu dữ liệu.
+ Lập bảng tần số tương đối:
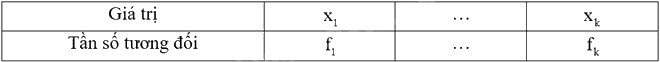
Trong đó và \({f_1}\) là tần số tương đối của \({x_1}\), …, \({f_k}\) là tần số tương đối của \({x_k}\).
Lời giải chi tiết:
a) Biểu đồ cột thể hiện: Tỉ lệ ủng hộ phương án 1 là 28%, Tỉ lệ ủng hộ phương án 2 là 61%, Tỉ lệ ủng hộ phương án 3 là 11%.
Biểu đồ hình quạt tròn thể hiện: Tỉ lệ ủng hộ phương án 1 là 28%, Tỉ lệ ủng hộ phương án 2 là 61%, Tỉ lệ ủng hộ phương án 3 là 11%.
b) Bảng tần số tương đối:

Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 39 SGK Toán 9 Kết nối tri thức
Có ba phương án thi đấu tại giải bóng đá khối lớp 9 của một trường như sau:
Phương án 1: Các đội đấu vòng tròn, tính điểm;
Phương án 2: Chia các đội thành hai bảng, mỗi bảng lấy hai đội vào trận bán kết;
Phương án 3: Các đội bốc thăm ghép cặp, đấu loại trực tiếp.
Ban tổ chức đã lấy phiếu khảo sát ý kiến. Kết quả được Bình và Nam biểu diễn bằng các biểu đồ như sau:
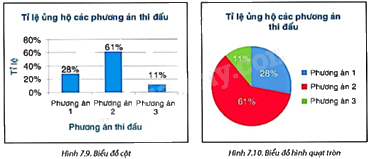
a) Đọc và giải thích mỗi biểu đồ trên.
b) Lập bảng tần số tương đối cho kết quả khảo sát ý kiến trên.
Phương pháp giải:
a) Chỉ ra tỉ lệ ủng hộ cho các phương án 1; 2; 3.
b) + Dựa vào biểu đồ chỉ ra tần số tương đối ứng với các giá trị trong mẫu dữ liệu.
+ Lập bảng tần số tương đối:
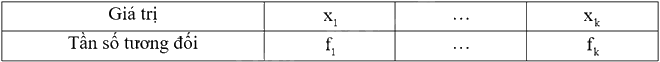
Trong đó và \({f_1}\) là tần số tương đối của \({x_1}\), …, \({f_k}\) là tần số tương đối của \({x_k}\).
Lời giải chi tiết:
a) Biểu đồ cột thể hiện: Tỉ lệ ủng hộ phương án 1 là 28%, Tỉ lệ ủng hộ phương án 2 là 61%, Tỉ lệ ủng hộ phương án 3 là 11%.
Biểu đồ hình quạt tròn thể hiện: Tỉ lệ ủng hộ phương án 1 là 28%, Tỉ lệ ủng hộ phương án 2 là 61%, Tỉ lệ ủng hộ phương án 3 là 11%.
b) Bảng tần số tương đối:

Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 41 SGK Toán 9 Kết nối tri thức
Bảng tần số tương đối sau cho biết tỉ lệ học sinh đánh giá độ khó của đề thi học kì môn Toán theo các mức độ.

Vẽ biểu đồ hình quạt tròn biểu diễn bảng tần số tương đối này.
Phương pháp giải:
Cách vẽ biểu đồ tần số tương đối:
Bước 1: Xác định số đo cung tương ứng của các hình quạt dùng để biểu diễn tần số tương đối của các giá trị theo công thức \({360^o}.{f_i}\) với \(i = 1,...,k\).
Bước 2: Vẽ hình tròn và chia hình tròn thành các hình quạt có số đo cung tương ứng được xác định trong Bước 1.
Bước 3: Định dạng các hình quạt tròn (thường bằng cách tô màu), ghi tần số tương đối, chú giải và tiêu đề.
Lời giải chi tiết:
Bước 1: Xác định số đo cung tương ứng của các hình quạt biểu diễn các tần số tương đối cho độ khó môn Toán:
Rất khó: \({360^o}.10\% = {36^o}\), khó: \({360^o}.25\% = {90^o}\), trung bình: \({360^o}.45\% = {162^o}\), dễ: \({360^o}.20\% = {72^o}\).
Bước 2: Vẽ hình tròn và chia hình tròn thành các hình quạt:
Bước 3: Định dạng các hình quạt tròn, ghi tỉ lệ phần trăm, chú giải và tiêu đề.
Video hướng dẫn giải
Trả lời câu hỏi Tranh luận trang 41 SGK Toán 9 Kết nối tri thức
Bạn Bình phát phiếu (H.7.13) lấy ý kiến bình chọn của 40 bạn trong lớp về địa điểm đi dã ngoại. Kết quả bạn Bình thu được như sau:


Vuông: Tớ sẽ dùng biểu đồ hình quạt tròn để biểu diễn bảng thống kê này.
Tròn: Không được. Cậu phải dùng biểu đồ cột để biểu diễn.
Ý kiến của bạn thế nào?
Phương pháp giải:
Sử dụng kiến thức về biểu đồ hình quạt tròn để giải thích.
Lời giải chi tiết:
Vì tổng số phần trăm tỉ lệ bình chọn của ba vườn quốc gia lớn hơn 100% nên không dùng biểu đồ hình quạt tròn để thể hiện bảng thống kê này được.
Có thể dùng biểu đồ cột để biểu diễn.
Mục 2 của chương trình Toán 9 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc hai. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 thường yêu cầu học sinh xác định các hệ số a, b, c của hàm số bậc hai y = ax2 + bx + c. Để làm bài này, các em cần nắm vững định nghĩa của hàm số bậc hai và biết cách nhận biết các hệ số tương ứng.
Bài 2 thường yêu cầu học sinh vẽ đồ thị của hàm số bậc hai. Để vẽ đồ thị, các em cần xác định đỉnh, trục đối xứng và các điểm đặc biệt của đồ thị. Việc sử dụng máy tính bỏ túi hoặc phần mềm vẽ đồ thị có thể giúp các em thực hiện bài này một cách nhanh chóng và chính xác.
Bài 3 thường yêu cầu học sinh tìm tập xác định và tập giá trị của hàm số bậc hai. Để tìm tập xác định, các em cần xác định các giá trị của x sao cho biểu thức trong hàm số có nghĩa. Để tìm tập giá trị, các em cần xác định giá trị lớn nhất hoặc nhỏ nhất của hàm số.
Bài 4 thường yêu cầu học sinh giải các phương trình bậc hai. Để giải phương trình bậc hai, các em có thể sử dụng công thức nghiệm hoặc phương pháp phân tích thành nhân tử. Việc lựa chọn phương pháp phù hợp sẽ giúp các em giải quyết bài toán một cách hiệu quả.
Bài 5 thường yêu cầu học sinh giải các bài toán ứng dụng liên quan đến hàm số bậc hai. Các bài toán này thường mô tả các tình huống thực tế và yêu cầu học sinh sử dụng kiến thức về hàm số bậc hai để tìm ra lời giải.
Khi giải bài tập về hàm số bậc hai, các em cần lưu ý một số điểm sau:
Hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải bài tập hiệu quả trên đây, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài tập trong mục 2 trang 39, 40, 41 SGK Toán 9 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!