Bài tập 9.44 trang 92 SGK Toán 9 tập 2 thuộc chương trình Kết nối tri thức là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng về hàm số bậc hai. Bài toán này thường yêu cầu học sinh xác định hệ số, tìm đỉnh parabol, vẽ đồ thị và ứng dụng vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 9.44 này, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
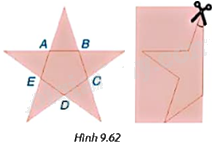
Bạn Lan muốn cắt hình ngôi sao có dạng như Hình 9.62 (trong đó ABCDE là một ngũ giác đều). Lan gấp đôi tờ giấy, vẽ một nửa ngôi sao và cắt theo nét vẽ. Góc tạo bởi lưỡi kéo và nếp gấp lúc đầu bằng bao nhiêu?
Đề bài
Bạn Lan muốn cắt hình ngôi sao có dạng như Hình 9.62 (trong đó ABCDE là một ngũ giác đều). Lan gấp đôi tờ giấy, vẽ một nửa ngôi sao và cắt theo nét vẽ. Góc tạo bởi lưỡi kéo và nếp gấp lúc đầu bằng bao nhiêu?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Tính được góc trong ngũ giác đều bằng \({108^o}\).
+ Tính được \(\widehat {HAB} = \widehat {HBA} = {180^o} - {108^o} = {72^o}\) nên \(\widehat {AHB} = {180^o} - \widehat {HAB} - \widehat {HBA} = {180^o} - {72^o} - {72^o} = {36^o}\)
+ Góc tạo bởi lưỡi kéo và nếp gấp lúc đầu bằng \(\frac{1}{2}\widehat {AHB} = \frac{1}{2}{.36^o} = {18^o}\).
Lời giải chi tiết
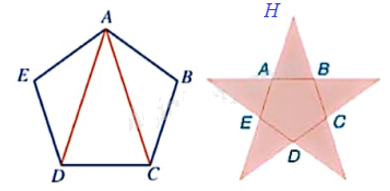
Xét ngũ giác đều ABCDE, ta thấy tổng 5 góc của ngũ giác đều đó bằng tổng các góc trong ba tam giác ABC, ACD, ADE, tức là bằng \({3.180^o} = {540^o}\). Do tất cả các góc của ngũ giác đều bằng nhau nên số đo mỗi góc của ngũ giác đều bằng \(\frac{{{{540}^o}}}{5} = {108^o}\).
Do đó, \(\widehat {EAB} = \widehat {ABC} = {108^o}\).
Suy ra: \(\widehat {HAB} = \widehat {HBA} = {180^o} - {108^o} = {72^o}\).
Tam giác HAB có:
\(\widehat {AHB} = {180^o} - \widehat {HAB} - \widehat {HBA} = {180^o} - {72^o} - {72^o} = {36^o}\)
Do đó, góc tạo bởi lưỡi kéo và nếp gấp lúc đầu là:
\(\frac{1}{2}\widehat {AHB} = \frac{1}{2}{.36^o} = {18^o}\).
Bài tập 9.44 trang 92 SGK Toán 9 tập 2 - Kết nối tri thức yêu cầu học sinh xét hàm số y = x2 - 4x + 3. Bài toán này bao gồm nhiều phần nhỏ, đòi hỏi học sinh phải nắm vững kiến thức về hàm số bậc hai, đặc biệt là các yếu tố như hệ số a, b, c, đỉnh parabol, trục đối xứng và giao điểm với các trục tọa độ.
Để giải bài tập này, trước tiên chúng ta cần xác định các yếu tố cơ bản của hàm số y = x2 - 4x + 3:
Việc xác định đúng các hệ số này là bước quan trọng để tính toán các yếu tố khác của hàm số.
Tọa độ đỉnh của parabol có dạng I(xI; yI), được tính theo công thức:
Vậy, tọa độ đỉnh của parabol là I(2; -1).
Trục đối xứng của parabol là đường thẳng có phương trình x = xI, tức là x = 2.
Để tìm giao điểm của parabol với trục hoành, ta giải phương trình y = 0:
x2 - 4x + 3 = 0
Phương trình này có thể được giải bằng cách sử dụng công thức nghiệm của phương trình bậc hai:
x = (-b ± √(b2 - 4ac)) / 2a = (4 ± √((-4)2 - 4 * 1 * 3)) / (2 * 1) = (4 ± √4) / 2
Vậy, ta có hai nghiệm:
Giao điểm của parabol với trục hoành là A(1; 0) và B(3; 0).
Để tìm giao điểm của parabol với trục tung, ta cho x = 0:
y = 02 - 4 * 0 + 3 = 3
Giao điểm của parabol với trục tung là C(0; 3).
Dựa vào các yếu tố đã tìm được (đỉnh, trục đối xứng, giao điểm với các trục tọa độ), ta có thể vẽ được đồ thị hàm số y = x2 - 4x + 3.
Thông qua việc giải bài tập 9.44 trang 92 SGK Toán 9 tập 2 - Kết nối tri thức, học sinh đã được củng cố kiến thức về hàm số bậc hai, bao gồm cách xác định các yếu tố của hàm số, tìm tọa độ đỉnh, trục đối xứng, giao điểm với các trục tọa độ và vẽ đồ thị hàm số. Việc nắm vững những kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình Toán 9.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài tập và tự tin hơn trong quá trình học tập. Chúc các em học tốt!