Bài học này cung cấp kiến thức nền tảng về bảng tần số, tần số tương đối, tần số ghép nhóm và các loại biểu đồ thường gặp trong chương trình Toán 9 Kết nối tri thức. Chúng ta sẽ cùng tìm hiểu cách xây dựng và phân tích bảng tần số, cách tính tần số tương đối và tần số ghép nhóm, cũng như cách lựa chọn biểu đồ phù hợp để biểu diễn dữ liệu.
Nội dung được trình bày một cách dễ hiểu, kèm theo các ví dụ minh họa cụ thể giúp học sinh nắm vững lý thuyết và áp dụng vào giải bài tập một cách hiệu quả.
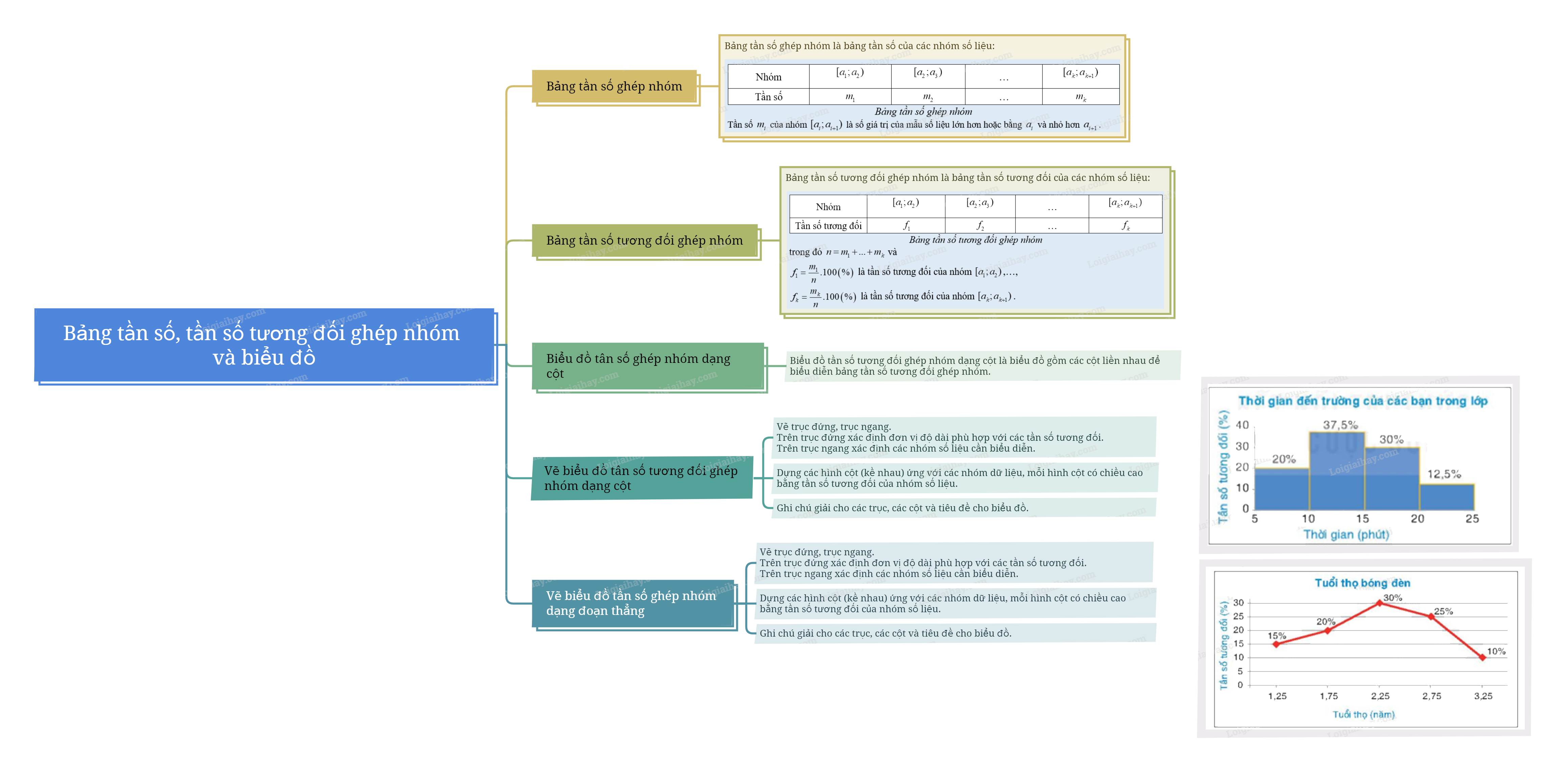
1. Bảng tần số, tần số tương đối ghép nhóm Bảng tần số ghép nhóm là bảng tần số của các nhóm số liệu:
1. Bảng tần số, tần số tương đối ghép nhóm
Bảng tần số ghép nhóm là bảng tần số của các nhóm số liệu:
Bảng tần số ghép nhóm Tần số \({m_i}\) của nhóm \({\rm{[}}{a_i};{a_{i + 1}})\) là số giá trị của mẫu số liệu lớn hơn hoặc bằng \({a_i}\) và nhỏ hơn \({a_{i + 1}}\). Bảng tần số tương đối ghép nhóm là bảng tần số tương đối của các nhóm số liệu:
Bảng tần số tương đối ghép nhóm trong đó \(n = {m_1} + ... + {m_k}\) và \({f_1} = \frac{{{m_1}}}{n}.100\left( \% \right)\) là tần số tương đối của nhóm \({\rm{[}}{a_1};{a_2})\),…, \({f_k} = \frac{{{m_k}}}{n}.100\left( \% \right)\) là tần số tương đối của nhóm \({\rm{[}}{a_k};{a_{k + 1}})\). |
Ví dụ: Với mẫu số liệu chiều cao (đơn vị là cm) của học sinh lớp 9A như sau:
156 157 164 166 166 165 157 156 155 158
160 163 163 161 162 159 159 160 160 160
159 158 160 160 158 163 162 162 162 161
162 161 163 161 163 161 164 166 165 165.
Số học sinh có chiều cao từ 155 cm đến dưới 158 cm là 5 học sinh;
từ 158 cm đến dưới 161 cm là 12 học sinh;
từ 161 đến dưới 164 cm là 15 học sinh;
từ 164 đến dưới 167 cm là 8 học sinh.
Do đó, tần số tương ứng với các nhóm là \(m{ _1} = 5,{m_2} = 12,{m_3} = 15,{m_4} = 8\).
Ta có bảng tần số ghép nhóm cho mẫu số này với các nhóm [155; 158), [158; 161), [161; 164), [164;167) là:

Tổng số học sinh của lớp \(n = 5 + 12 + 15 + 8 = 40\).
Tỉ số học sinh có chiều cao từ 150 cm đến dưới 158 cm là \(\frac{5}{{40}} = 12,5\% \);
từ 158 cm đến dưới 161 cm là \(\frac{{12}}{{40}} = 30\% \);
từ 161 đến dưới 164 cm là \(\frac{{15}}{{40}} = 37,5\% \);
từ 164 đến dưới 167 cm là \(\frac{8}{{40}} = 20\% \).
Bảng tần số tương đối ghép nhóm cho mẫu số này với các nhóm [155; 158), [158; 161), [161; 164), [164;167) là:

2. Biểu đồ tần số tương đối ghép nhóm dạng cột
• Biểu đồ tần số tương đối ghép nhóm dạng cột là biểu đồ gồm các cột liền nhau để biểu diễn bảng tần số tương đối ghép nhóm. Trong biểu đồ này, chiều cao mỗi cột biểu diễn tần số tương đối của nhóm số liệu. • Để vẽ biểu đồ tần số tương đối ghép nhóm dạng cột biểu diễn bảng tần số tương đối ghép nhóm với các nhóm số liệu có độ dài bằng nhau ta thực hiện theo các bước sau: Bước 1. Vẽ trục đứng, trục ngang. Trên trục đứng xác định đơn vị độ dài phù hợp với các tần số tương đối. Trên trục ngang xác định các nhóm số liệu cần biểu diễn. Bước 2. Dựng các hình cột (kề nhau) ứng với các nhóm dữ liệu, mỗi hình cột có chiều cao bằng tần số tương đối của nhóm số liệu. Bước 3. Ghi chú giải cho các trục, các cột và tiêu đề cho biểu đồ. |
Biểu đồ tần số tương đối (tần số) ghép nhóm dạng cột còn gọi là tổ chức đồ (histogram).
Ví dụ: Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột cho bảng thống kê về thời gian đi từ nhà tới trường của một số bạn trong lớp 9D.

Bước 1. Vẽ các trục của biểu đồ, xác định đơn vị độ dài trên trục đứng, các nhóm trên trục ngang.
Bước 2. Dựng các hình cột kề nhau ứng với các nhóm số liệu.
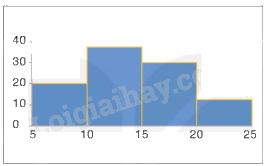
Bước 3. Ghi chú giải cho các trục, các cột và tiêu đề của biểu đồ.
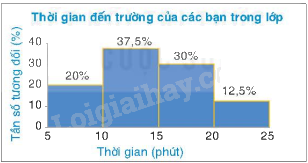
2. Biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng
Cách vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng
Để vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng cho mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau: Bước 1. Chọn giá trị \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) đại diện cho nhóm số liệu \({\rm{[}}{a_i};{a_{i + 1}})\) với \(i = 1,2,...,k\). Bước 2. Vẽ trục ngang để biểu diễn các giá trị đại diện cho các nhóm số liệu, vẽ trục đứng thể hiện tần số tương đối. Bước 3. Với mỗi giá trị đại diện x, trên trục ngang và tần số tương đối \({f_i}\) tương ứng, ta xác định một điểm \({M_i}\left( {{x_i};{f_i}} \right)\). Nối các điểm liên tiếp với nhau. Bước 4. Ghi chú giải cho các trục, các điểm và tiêu đề của biểu đồ. |
Chú ý: Trong cách vẽ biểu đồ trên, nếu thay tần số tương đối bằng tần số thì ta có biểu đồ tần số ghép nhóm dạng đoạn thẳng.
Ví dụ: Vẽ biểu đồ tương đối ghép nhóm dạng đoạn thẳng cho bảng tần số tương đối ghép nhóm về tuổi thọ của một loại bóng đèn:

Bước 1. Chọn giá trị đại diện cho các nhóm số liệu ta có bảng sau:

Bước 2. Vẽ các trục.
Bước 3. Xác định các điểm, nối các điểm liên tiếp với nhau.
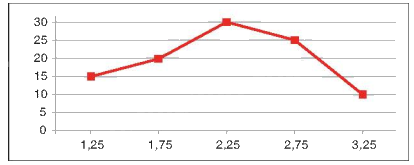
Bước 4. Ghi chú giải cho các trục, các điểm và tiêu đề cho biểu đồ tần số tương đối ghép nhóm
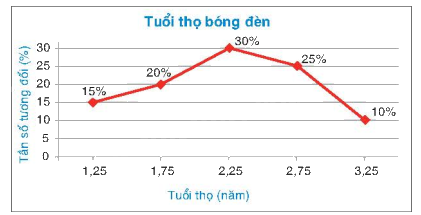
Chú ý: Trên trục ngang ta cũng có thể điền các nhóm số liệu thay cho các giá trị đại diện.
Trong chương trình Toán 9 Kết nối tri thức, việc nắm vững kiến thức về thống kê và xử lý dữ liệu là vô cùng quan trọng. Một trong những công cụ cơ bản và hữu ích nhất trong thống kê là bảng tần số. Bảng tần số giúp chúng ta tổ chức và tóm tắt một tập dữ liệu lớn một cách khoa học và dễ dàng phân tích.
Bảng tần số là một bảng liệt kê các giá trị khác nhau trong một tập dữ liệu cùng với số lần xuất hiện của mỗi giá trị đó (gọi là tần số). Bảng tần số giúp chúng ta nhanh chóng nhận biết được các giá trị phổ biến nhất và các giá trị ít xuất hiện nhất trong tập dữ liệu.
Ví dụ: Giả sử chúng ta có một tập dữ liệu về điểm kiểm tra Toán của 20 học sinh:
Bảng tần số của tập dữ liệu này sẽ như sau:
| Điểm | Tần số |
|---|---|
| 5 | 4 |
| 6 | 4 |
| 7 | 5 |
| 8 | 4 |
| 9 | 3 |
Tần số tương đối là tỷ lệ giữa tần số của một giá trị và tổng số các giá trị trong tập dữ liệu. Tần số tương đối thường được biểu diễn dưới dạng phần trăm.
Công thức: Tần số tương đối = (Tần số của giá trị) / (Tổng số các giá trị)
Ví dụ: Sử dụng bảng tần số ở trên, tần số tương đối của điểm 7 là: 5 / 20 = 0.25 hay 25%.
Khi tập dữ liệu có nhiều giá trị khác nhau, việc liệt kê tất cả các giá trị vào bảng tần số có thể trở nên phức tạp. Trong trường hợp này, chúng ta có thể sử dụng phương pháp ghép nhóm để giảm số lượng các giá trị khác nhau trong bảng tần số.
Ví dụ: Thay vì liệt kê từng điểm số riêng lẻ, chúng ta có thể ghép các điểm số vào các khoảng, ví dụ:
Bảng tần số ghép nhóm sẽ như sau:
| Khoảng | Tần số |
|---|---|
| 5-6 | 8 |
| 7-8 | 9 |
| 9-10 | 3 |
Biểu đồ là một cách trực quan để biểu diễn dữ liệu. Có nhiều loại biểu đồ khác nhau, mỗi loại phù hợp với một loại dữ liệu khác nhau.
Việc lựa chọn biểu đồ phù hợp sẽ giúp chúng ta dễ dàng nhận biết được các xu hướng và mối quan hệ trong dữ liệu.
Các khái niệm này có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, bao gồm:
Việc hiểu rõ và áp dụng thành thạo các kiến thức này sẽ giúp bạn xử lý dữ liệu một cách hiệu quả và đưa ra các quyết định sáng suốt.