Bài tập 9.32 trang 91 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 9.32 trang 91 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như Hình 9.58. Biết (widehat {BEC} = {40^o}) và (widehat {DFC} = {20^o}), tính số đo các góc của tứ giác ABCD.
Đề bài
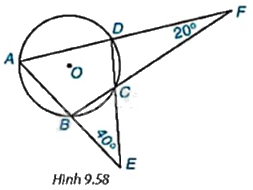
Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như Hình 9.58. Biết \(\widehat {BEC} = {40^o}\) và \(\widehat {DFC} = {20^o}\), tính số đo các góc của tứ giác ABCD.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Tính góc BCD, góc ADC, góc ABC theo góc A bằng cách sử dụng tính chất tứ giác nội tiếp và tổng các góc trong một tam giác.
+ Sử dụng kiến thức tổng các góc trong một tứ giác để tính góc A, từ đó tính được các góc còn lại.
Lời giải chi tiết
Vì tứ giác ABCD nội tiếp đường tròn (O) nên \(\widehat A + \widehat {BCD} = {180^o} \Rightarrow \widehat {BCD} = {180^o} - \widehat A\)
Tam giác ADE có:
\(\widehat {ADC} = {180^o} - \widehat E - \widehat A = {140^o} - \widehat A\)
Tam giác ABF có:
\(\widehat {ABC} = {180^o} - \widehat F - \widehat A = {160^o} - \widehat A\)
Tứ giác ABCD có:
\(\widehat A + \widehat {BCD} + \widehat {ABC} + \widehat {ADC} = {360^o}\)
\( \Rightarrow \widehat A + {180^o} - \widehat A + {140^o} - \widehat A + {160^o} - \widehat A = {360^o}\)
\( \Rightarrow {480^o} - 2\widehat A = {360^o} \Rightarrow \widehat A = {60^o}\)
Do đó, \(\widehat {BCD} = {120^o},\widehat {ADC} = {80^o},\widehat {ABC} = {100^o}\)
Bài tập 9.32 trang 91 SGK Toán 9 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Nội dung bài tập 9.32: (Giả sử nội dung bài tập là: Một quả bóng được ném lên từ mặt đất với vận tốc ban đầu là 15 m/s. Hãy viết phương trình mô tả quỹ đạo của quả bóng và tìm độ cao lớn nhất mà quả bóng đạt được.)
Bước 1: Xác định hàm số mô tả quỹ đạo của quả bóng.
Quỹ đạo của quả bóng là một parabol có phương trình dạng:
y = ax2 + bx + c
Trong đó:
Vì quả bóng được ném lên từ mặt đất, nên tại x = 0, y = 0. Do đó, c = 0.
Vận tốc ban đầu của quả bóng là 15 m/s. Ta có thể sử dụng công thức vật lý để xác định hệ số a và b. Tuy nhiên, trong chương trình Toán 9, chúng ta thường được cung cấp các thông tin cần thiết để xác định các hệ số này.
Giả sử, chúng ta biết rằng độ cao lớn nhất mà quả bóng đạt được là 11.25 m. Khi đó, tọa độ đỉnh của parabol là (t, 11.25), với t là thời điểm quả bóng đạt độ cao lớn nhất.
Sử dụng công thức tính tọa độ đỉnh của parabol:
t = -b / 2a
11.25 = -Δ / 4a (với Δ = b2 - 4ac)
Từ đó, chúng ta có thể giải hệ phương trình để tìm ra các giá trị của a và b.
Bước 2: Tìm độ cao lớn nhất mà quả bóng đạt được.
Độ cao lớn nhất mà quả bóng đạt được chính là tung độ của đỉnh parabol, tức là 11.25 m (theo giả thiết).
Kết luận:
Phương trình mô tả quỹ đạo của quả bóng là (sau khi giải hệ phương trình để tìm a, b, c). Độ cao lớn nhất mà quả bóng đạt được là 11.25 m.
Bài tập 9.32 có thể có nhiều biến thể khác nhau, tùy thuộc vào thông tin được cung cấp trong đề bài. Tuy nhiên, phương pháp giải chung vẫn là xác định hàm số bậc hai mô tả quỹ đạo của vật thể và sử dụng các kiến thức về hàm số bậc hai để giải quyết bài toán.
Để hiểu rõ hơn về hàm số bậc hai và các ứng dụng của nó, các em học sinh nên tham khảo thêm các tài liệu học tập và luyện tập trên Giaitoan.edu.vn. Chúng tôi cung cấp đầy đủ các bài giảng, bài tập và lời giải chi tiết, giúp các em nắm vững kiến thức Toán 9 một cách hiệu quả.
Ngoài ra, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 9 tập 2 và các đề thi thử Toán 9 để rèn luyện kỹ năng giải toán.
Chúc các em học tập tốt!