Bài tập 9.13 trang 79 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 9.13 trang 79 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Cho tam giác ABC nội tiếp đường tròn (O). Biết rằng (widehat {BOC} = {120^o}) và (widehat {OCA} = {20^o}). Tính số đo các góc của tam giác ABC.
Đề bài
Cho tam giác ABC nội tiếp đường tròn (O). Biết rằng \(\widehat {BOC} = {120^o}\) và \(\widehat {OCA} = {20^o}\). Tính số đo các góc của tam giác ABC.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Tính được \(\widehat {BAC} = \frac{1}{2}\widehat {BOC} = \frac{1}{2}{.120^o} = {60^o}\).
+ Chứng minh tam giác AOC cân tại O, tính được: \(\widehat {ACO} = \widehat {OAC}\)
+ Tính được \(\widehat {AOC} = {180^o} - \widehat {CAO} - \widehat {ACO}\)
+ Tính được \(\widehat {ABC} = \frac{1}{2}\widehat {AOC} = \frac{1}{2}{.140^o} = {70^o}\)
+ Tam giác ABC có: \(\widehat {ACB} = {180^o} - \widehat {BAC} - \widehat {ABC}\)
Lời giải chi tiết
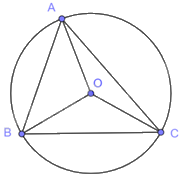
Tam giác ACO có: \(OA = OC\) (bán kính (O)) nên tam giác AOC cân tại O. Do đó, \(\widehat {ACO} = \widehat {OAC} = {20^o}\)
Suy ra:
\(\widehat {AOC} = {180^o} - \widehat {CAO} - \widehat {ACO} = {180^o} - {20^o} - {20^o} = {140^o}\)
Xét đường tròn (O):
Vì góc nội tiếp BAC và góc ở tâm BOC cùng chắn cung nhỏ BC nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC} = \frac{1}{2}{.120^o} = {60^o}\)
Vì góc nội tiếp ABC và góc ở tâm AOC cùng chắn cung nhỏ AC nên \(\widehat {ABC} = \frac{1}{2}\widehat {AOC} = \frac{1}{2}{.140^o} = {70^o}\)
Tam giác ABC có:
\(\widehat {ACB} = {180^o} - \widehat {BAC} - \widehat {ABC} = {180^o} - {60^o} - {70^o} = {50^o}\)
Bài tập 9.13 SGK Toán 9 tập 2 Kết nối tri thức là một bài toán ứng dụng thực tế về hàm số bậc hai. Để giải bài toán này, học sinh cần nắm vững các kiến thức sau:
Nội dung bài tập:
Một người nông dân muốn xây một chuồng trại hình chữ nhật có diện tích 300m2. Người đó có 60m hàng rào để làm hàng rào xung quanh chuồng trại. Hỏi chuồng trại có chiều dài và chiều rộng là bao nhiêu để sử dụng hết hàng rào và diện tích chuồng trại là lớn nhất?
Bước 1: Đặt ẩn và biểu diễn các đại lượng theo ẩn
Gọi chiều dài của chuồng trại là x (m) và chiều rộng là y (m). Điều kiện: x > 0, y > 0.
Diện tích chuồng trại là xy = 300 (m2).
Chu vi chuồng trại là 2(x + y) = 60 (m).
Bước 2: Giải hệ phương trình
Từ xy = 300, ta có y = 300/x.
Thay vào 2(x + y) = 60, ta được 2(x + 300/x) = 60.
Suy ra x + 300/x = 30.
Nhân cả hai vế với x, ta được x2 + 300 = 30x.
Chuyển vế, ta được x2 - 30x + 300 = 0.
Giải phương trình bậc hai này, ta có Δ = (-30)2 - 4(1)(300) = 900 - 1200 = -300 < 0.
Vì Δ < 0, phương trình vô nghiệm. Điều này có nghĩa là không có chuồng trại hình chữ nhật nào có diện tích 300m2 và chu vi 60m.
Lưu ý: Đề bài có thể có sai sót. Nếu đề bài yêu cầu diện tích lớn nhất với một lượng hàng rào cố định, ta cần giải bài toán tối ưu hóa.
Giả sử người nông dân có 60m hàng rào và muốn xây chuồng trại hình chữ nhật có diện tích lớn nhất.
Ta có 2(x + y) = 60, suy ra x + y = 30, hay y = 30 - x.
Diện tích chuồng trại là S = xy = x(30 - x) = 30x - x2.
Để tìm diện tích lớn nhất, ta tìm giá trị lớn nhất của hàm số S(x) = 30x - x2.
Hàm số S(x) là hàm bậc hai có hệ số a = -1 < 0, nên hàm số đạt giá trị lớn nhất tại đỉnh của parabol.
Hoành độ đỉnh là x = -b/(2a) = -30/(2(-1)) = 15.
Khi x = 15, y = 30 - 15 = 15.
Vậy diện tích lớn nhất của chuồng trại là S = 15 * 15 = 225 m2.
Kết luận:
Nếu đề bài yêu cầu diện tích cố định, bài toán vô nghiệm. Nếu đề bài yêu cầu diện tích lớn nhất với chu vi cố định, chuồng trại có hình vuông với cạnh 15m và diện tích 225m2.