Chào mừng bạn đến với bài học lý thuyết về căn bậc hai và căn thức bậc hai trong chương trình Toán 9 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về chủ đề này.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, điều kiện xác định, các tính chất và ứng dụng của căn bậc hai và căn thức bậc hai. Đồng thời, bài học cũng sẽ giúp bạn rèn luyện kỹ năng giải các bài tập liên quan.
1. Căn bậc hai Khái niệm căn bậc hai
1. Căn bậc hai
Khái niệm căn bậc hai
Căn bậc hai của số thực không âm a là số thực x sao cho \({x^2} = a\). |
Nhận xét:
- Số âm không có căn bậc hai.
- Số 0 có một căn bậc hai duy nhất là 0.
- Số dương a có đúng hai căn bậc hai đối nhau là \(\sqrt a \) (căn bậc hai số học của a) và \( - \sqrt a \).
Ví dụ:
Tính căn bậc hai của một số bằng máy tính cầm tay
Để tính các căn bậc hai của một số \(a > 0\), chỉ cần tính \(\sqrt a \). Có thể dễ dàng làm điều này bằng cách sử dụng MTCT.
Sử dụng nút này để bấm căn bậc hai. |
Ví dụ:
Bấm lần lượt các phím ta tính được \(\sqrt {11,1} \approx 3,33\).
Vậy căn bậc hai của 11,1 (làm tròn đến chữ số thập phân thứ hai) là 3,33 và -3,33.
Tính chất của căn bậc hai
\(\sqrt {{a^2}} = \left| a \right|\) với mọi số thực a. |
Ví dụ: \(\sqrt {{{\left( {1 + \sqrt 2 } \right)}^2}} = \left| {1 + \sqrt 2 } \right| = 1 + \sqrt 2 \); \(\sqrt {{{\left( { - 3} \right)}^2}} = \left| { - 3} \right| = 3\).
2. Căn thức bậc hai
Khái niệm căn thức bậc hai
Căn thức bậc hai là biểu thức có dạng \(\sqrt A \), trong đó A là một biểu thức đại số. A được gọi là biểu thức lấy căn hoặc biểu thức dưới dấu căn. |
Ví dụ: \(\sqrt {2x - 1} \), \(\sqrt { - \frac{1}{3}x + 2} \) là các căn thức bậc hai.
Điều kiện xác định của căn thức bậc hai
\(\sqrt A \) xác định khi A lấy giá trị không âm và ta thường viết là \(A \ge 0\). Ta nói \(A \ge 0\) là điều kiện xác định (hay điều kiện có nghĩa) của \(\sqrt A \). |
Ví dụ: Điều kiện xác định của căn thức \(\sqrt {2x + 1} \) là \(2x + 1 \ge 0\) hay \(x \ge - \frac{1}{2}\).
Điều kiện xác định của căn thức \(\sqrt { - \frac{1}{3}x + 2} \) là \( - \frac{1}{3}x + 2 \ge 0\) hay \(x \le 6\).
Hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\)
Với A là một biểu thức, ta có:
|
Ví dụ: Với \(x < 0\), ta có 1 – x > 0. Do đó \({\left( {\sqrt {1 - x} } \right)^2} = 1 - x\).
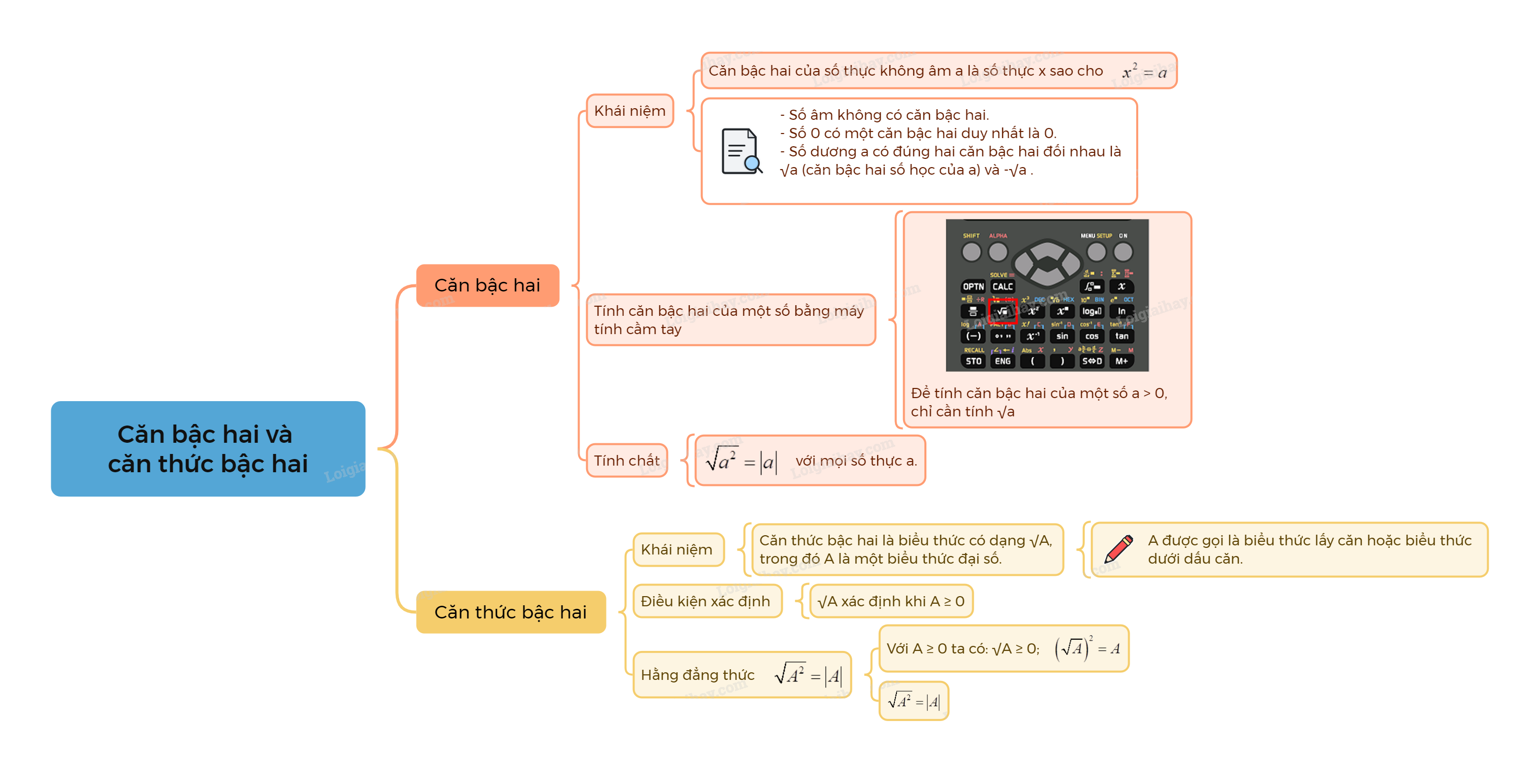
Căn bậc hai và căn thức bậc hai là một trong những chủ đề quan trọng trong chương trình Toán 9, đặc biệt là chương trình Kết nối tri thức. Việc nắm vững lý thuyết và kỹ năng giải bài tập liên quan đến chủ đề này là rất cần thiết để đạt kết quả tốt trong các kỳ thi và chuẩn bị cho các kiến thức nâng cao hơn.
Định nghĩa: Căn bậc hai của một số a không âm là số x sao cho x2 = a. Ký hiệu: √a.
Điều kiện xác định: √a xác định khi và chỉ khi a ≥ 0.
Tính chất:
Định nghĩa: Căn thức bậc hai của biểu thức A là biểu thức có dạng √A, trong đó A là một biểu thức đại số.
Điều kiện xác định: √A xác định khi và chỉ khi A ≥ 0.
Các phép biến đổi căn thức:
Căn bậc hai là một trường hợp đặc biệt của căn thức bậc hai, trong đó biểu thức dưới dấu căn là một số. Căn thức bậc hai có thể chứa các biểu thức đại số phức tạp hơn, bao gồm các biến số và các phép toán khác.
Ví dụ 1: Tính √(16) = 4
Ví dụ 2: Rút gọn biểu thức √(25x2) = 5|x|
Ví dụ 3: Đưa thừa số vào trong dấu căn: 2√3 = √12
Căn bậc hai và căn thức bậc hai được ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học, bao gồm:
Khi làm việc với căn bậc hai và căn thức bậc hai, cần lưu ý các điều sau:
Hy vọng bài học này đã cung cấp cho bạn những kiến thức cơ bản và quan trọng về lý thuyết căn bậc hai và căn thức bậc hai Toán 9 Kết nối tri thức. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải các bài tập thực tế.