Bài tập 7.4 trang 37 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 7.4 trang 37 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất bài toán và tự tin làm bài.
Người ta thống kê các loại ô tô chạy qua một trạm thu phí trong 1 giờ và vẽ được biểu đồ tần số như Hình 7.8. a) Lập bảng tần số cho dữ liệu được biểu diễn trên biểu đồ; b) Từ bảng tần số, hãy cho biết loại xe nào đi qua trạm thu phí nhiều nhất.
Đề bài
Người ta thống kê các loại ô tô chạy qua một trạm thu phí trong 1 giờ và vẽ được biểu đồ tần số như Hình 7.8.
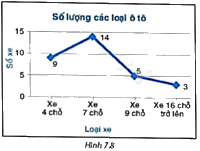
a) Lập bảng tần số cho dữ liệu được biểu diễn trên biểu đồ;
b) Từ bảng tần số, hãy cho biết loại xe nào đi qua trạm thu phí nhiều nhất.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) + Dựa vào biểu đồ, liệt kê số xe có 4 chỗ, 7 chỗ, 9 chỗ và 16 chỗ trở lên.
+ Bảng tần số có dạng bảng sau:

Trong đó, \({m_1}\) là tần số của \({x_1}\), \({m_2}\) là tần số của \({x_2}\),…, \({m_k}\) là tần số của \({x_k}\).
Trong bảng tần số, ta chỉ liệt kê các giá trị \({x_i}\) khác nhau, các giá trị \({x_i}\) này có thể không là số.
b) Loại xe nào có tần số lớn nhất thì đi qua trạm thu phí nhiều nhất.
Lời giải chi tiết
a) Theo biểu đồ, ta thấy có 9 xe 4 chỗ, 14 xe 7 chỗ, 5 xe 9 chỗ và 3 xe 16 chỗ trở lên.
Ta có bảng tần số:

b) Vì \(14 > 9 > 5 > 3\) nên xe 7 chỗ đi qua trạm thu phí nhiều nhất.
Bài tập 7.4 trang 37 SGK Toán 9 tập 2 yêu cầu giải bài toán về việc tìm số tiền mà mỗi bạn An và Bình có, dựa trên thông tin về tổng số tiền và mối quan hệ giữa số tiền của hai bạn. Để giải bài toán này, chúng ta sẽ sử dụng phương pháp giải hệ phương trình bậc nhất hai ẩn.
An và Bình có tổng cộng 120 nghìn đồng. Nếu An cho Bình 20 nghìn đồng thì số tiền của Bình gấp đôi số tiền của An. Hỏi lúc đầu mỗi bạn có bao nhiêu tiền?
1. Đặt ẩn:
2. Lập phương trình:
Dựa vào đề bài, ta có hệ phương trình sau:
| Phương trình | Giải thích |
|---|---|
| x + y = 120 | Tổng số tiền của An và Bình là 120 nghìn đồng. |
| y + 20 = 2(x - 20) | Sau khi An cho Bình 20 nghìn đồng, số tiền của Bình gấp đôi số tiền của An. |
3. Giải hệ phương trình:
Ta có hệ phương trình:
x + y = 120
y + 20 = 2(x - 20)
Giải hệ phương trình này, ta được:
4. Kết luận:
Vậy lúc đầu An có 60 nghìn đồng và Bình có 60 nghìn đồng.
Bài tập về hệ phương trình bậc nhất hai ẩn có nhiều ứng dụng trong thực tế, như giải các bài toán về chuyển động, tính tuổi, tính giá cả,... Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp các em học sinh giải quyết các vấn đề thực tế một cách hiệu quả.
Để luyện tập thêm, các em có thể tham khảo các bài tập tương tự trong SGK Toán 9 tập 2 và các tài liệu ôn tập khác. Giaitoan.edu.vn sẽ tiếp tục cập nhật thêm nhiều lời giải chi tiết cho các bài tập Toán 9 khác, giúp các em học tập tốt hơn.
Hy vọng với lời giải chi tiết này, các em học sinh đã hiểu rõ cách giải bài tập 7.4 trang 37 SGK Toán 9 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!