Bài tập 5.20 trang 103 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Đây là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 5.20 này, giúp các em học sinh hiểu rõ phương pháp giải và tự tin hơn trong quá trình học tập.
Bạn Thanh cắt 4 hình tròn bằng giấy có bán kính lần lượt là 4 cm, 6 cm, 7 cm và 8 cm để dán trang trí trên một mảnh giấy, trên đó có vẽ trước hai đường thẳng a và b.
Đề bài
Bạn Thanh cắt 4 hình tròn bằng giấy có bán kính lần lượt là 4 cm, 6 cm, 7 cm và 8 cm để dán trang trí trên một mảnh giấy, trên đó có vẽ trước hai đường thẳng a và b. Biết rằng a và b là hai đường thẳng song song với nhau và cách nhau một khoảng 6 cm (nghĩa là mọi điểm trên đường thẳng b đều cách a một khoảng 6 cm). Hỏi nếu bạn Thanh dán sao cho tâm của cả 4 hình tròn đều nằm trên đường thẳng b thì hình tròn nào sẽ che khuất một phần của đường thẳng a, hình tròn nào sẽ không che khuất một phần của đường thẳng a?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Cho đường thẳng a và đường tròn (O; R). Gọi d là khoảng cách từ O đến a. Khi đó:
+ Đường thẳng a và đường tròn (O; R) cắt nhau khi \(d < R\).
+ Đường thẳng a và đường tròn (O; R) tiếp xúc với nhau khi \(d = R\).
+ Đường thẳng a và đường tròn (O; R) không giao nhau khi \(d > R\).
Lời giải chi tiết
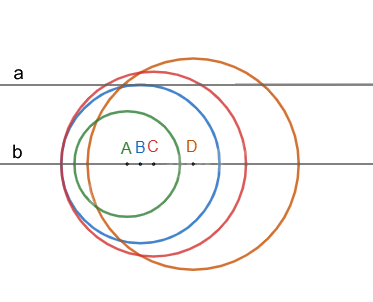
Giả sử bốn hình tròn bằng giấy có tâm lần lượt là A, B, C và D. Khi đó, ta có các đường tròn (A; 4cm), (B; 6cm), (C; 7cm), (D; 8cm). Tâm của các đường tròn này thuộc đường thẳng b nên đều cách a một khoảng \(d = 6cm\).
+ Đường tròn (A; 4cm) có bán kính 4cm < d nên đường tròn (A; 4cm) không giao đường thẳng a.
+ Đường tròn (B; 6cm) có bán kính 6cm=d nên đường tròn (B; 6cm) tiếp xúc với đường thẳng a.
+ Đường tròn (C; 7cm) có bán kính 7cm>d nên đường tròn (C; 7cm) cắt đường thẳng a.
+ Đường tròn (D; 8cm) có bán kính 8cm>d nên đường tròn (D; 8cm) cắt đường thẳng a.
Từ đó các hình tròn bán kính 4cm, 6cm không đè lên đường thẳng a; các hình tròn bán kính 7cm, 8cm đè lên đường thẳng a.
Bài tập 5.20 SGK Toán 9 tập 1 - Kết nối tri thức yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc nhất. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Nội dung bài tập 5.20: (Giả sử nội dung bài tập là: Một người đi xe đạp từ A đến B với vận tốc 12km/h. Hỏi người đó đi hết bao lâu nếu quãng đường AB dài 36km?)
Lời giải:
Gọi t (giờ) là thời gian người đó đi từ A đến B.
Quãng đường AB dài 36km, vận tốc của người đi xe đạp là 12km/h. Ta có công thức:
Quãng đường = Vận tốc × Thời gian
36 = 12 × t
t = 36 / 12 = 3 (giờ)
Vậy người đó đi hết 3 giờ để đi từ A đến B.
Phân tích lời giải:
Trong bài tập này, chúng ta đã sử dụng công thức quãng đường = vận tốc × thời gian để giải quyết bài toán. Việc hiểu rõ mối quan hệ giữa các đại lượng này là rất quan trọng để giải quyết các bài toán thực tế liên quan đến hàm số bậc nhất.
Các bài tập tương tự:
Lưu ý khi giải bài tập về hàm số bậc nhất:
Ứng dụng của hàm số bậc nhất trong thực tế:
Hàm số bậc nhất được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như:
Hy vọng với lời giải chi tiết và những phân tích trên, các em học sinh đã hiểu rõ cách giải bài tập 5.20 trang 103 SGK Toán 9 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!
Ví dụ minh họa bằng bảng:
| Thời gian (giờ) | Quãng đường (km) |
|---|---|
| 1 | 12 |
| 2 | 24 |
| 3 | 36 |
Bảng trên cho thấy mối quan hệ giữa thời gian và quãng đường khi vận tốc không đổi là 12km/h.
Kết luận:
Bài tập 5.20 là một ví dụ điển hình về ứng dụng của hàm số bậc nhất trong thực tế. Việc nắm vững kiến thức về hàm số bậc nhất sẽ giúp các em giải quyết các bài toán tương tự một cách dễ dàng và hiệu quả.