Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 4.7 trang 73 SGK Toán 9 tập 1 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em học sinh nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Dùng MTCT, tìm số đo của góc nhọn x (làm tròn đến phút) , biết rằng: a) (sin x = 0,2368;) b) (cos x = 0,6224;) c) (tan x = 1,236;) d) (cot x = 2,154.)
Đề bài
Dùng MTCT, tìm số đo của góc nhọn x (làm tròn đến phút) , biết rằng:
a) \(\sin x = 0,2368;\)
b) \(\cos x = 0,6224;\)
c) \(\tan x = 1,236;\)
d) \(\cot x = 2,154.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Để tìm góc \(x\) khi biết \(\sin x = 0,2368\) thì ta bấm MTCT:
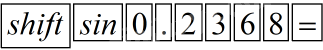
ta được kết quả 13,6977504 thì ta bấm tiếp 0’’’ ta được kết quả \({13^0}41'51,9'' \approx {13^0}42'\) tương tự đối với trường hợp cos và tan. Tuy nhiên đối với trường hợp tìm \(x\) khi biết \(\cot x\) thì ta có thể tìm góc \({90^0} - x\) (vì \(\tan \left( {{{90}^0} - x} \right) = \cot x\) từ đó ta tính được \(x\)) .
Lời giải chi tiết
a) \(\sin x = 0,2368;\)
Ta có: \(\sin x = 0,2368\) nên \(x = {13^0}41'51,9'' \approx {13^0}42'\)
b) \(\cos x = 0,6224;\)
Ta có: \(\cos x = 0,6224\) nên \(x = {51^0}30'30,21'' \approx {51^0}31'\)
c) \(\tan x = 1,236;\)
Ta có: \(\tan x = 1,236\) nên \(x = {51^0}1'30,04'' \approx {51^0}2'\)
d) \(\cot x = 2,154.\)
Ta có: \(\cot x = 2,154\) nên \(x = {24^0}54'11,54'' \approx {24^0}54'\)
Bài tập 4.7 trang 73 SGK Toán 9 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 9, tập trung vào việc vận dụng kiến thức về hàm số bậc nhất và ứng dụng của nó trong thực tế. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản và các phương pháp giải phù hợp.
Bài tập 4.7 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc nhất. Cụ thể, bài toán thường mô tả một tình huống trong đó có một đại lượng thay đổi theo một đại lượng khác, và yêu cầu học sinh xác định hàm số biểu diễn mối quan hệ đó, sau đó sử dụng hàm số để giải các câu hỏi liên quan.
Đề bài: Một người đi xe máy từ A đến B với vận tốc 40 km/h. Hỏi sau bao lâu người đó đến B nếu quãng đường AB dài 120 km?
Giải:
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ như:
Để hiểu rõ hơn về hàm số bậc nhất và các ứng dụng của nó, bạn có thể tham khảo thêm các tài liệu sau:
Bài tập 4.7 trang 73 SGK Toán 9 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và ứng dụng của nó trong thực tế. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ giải bài tập này một cách dễ dàng và hiệu quả.