Bài tập 9.41 trang 92 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trong quá trình học tập, cung cấp các tài liệu học tập chất lượng, lời giải bài tập chính xác và nhanh chóng.
Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp.
Đề bài
Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Chứng minh được \(OM \bot BC,ON \bot AC,OP \bot AB\).
+ Chứng minh \(\Delta \)ANO vuông tại N và \(\Delta \)AOP vuông tại P nên tứ giác ANOP là tứ giác nội tiếp.
+ Chứng minh \(\Delta \)CNO vuông tại N và \(\Delta \)COM vuông tại M nên tứ giác CMON là tứ giác nội tiếp.
+ Chứng minh \(\Delta \)MOB vuông tại M và \(\Delta \)BOP vuông tại P nên tứ giác BPOM là tứ giác nội tiếp.
Lời giải chi tiết
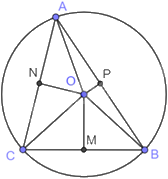
\(\Delta \)AOB có \(OA = OB\) (bán kính đường tròn (O)) nên \(\Delta \)OAB cân tại O, OP là đường trung tuyến đồng thời là đường cao. Suy ra: \(OP \bot AB\) nên \(\Delta \)OPA vuông tại P và \(\Delta \)OBP vuông tại P.
Chứng minh tương tự ta có: \(\Delta \)MOB vuông tại M, \(\Delta \)COM vuông tại M, \(\Delta \)NOC vuông tại N, \(\Delta \)NOA vuông tại N.
Vì \(\Delta \)OPA vuông tại P nên P thuộc đường tròn đường kính AO, \(\Delta \)NOA vuông tại N nên N thuộc đường tròn đường kính AO. Do đó, tứ giác ANOP nội tiếp đường tròn đường kính AO.
Vì \(\Delta \)OPB vuông tại P nên P thuộc đường tròn đường kính BO, \(\Delta \)MOB vuông tại M nên M thuộc đường tròn đường kính BO. Do đó, tứ giác BPOM nội tiếp đường tròn đường kính BO.
Vì \(\Delta \)COM vuông tại M nên M thuộc đường tròn đường kính CO, \(\Delta \)NOC vuông tại N nên N thuộc đường tròn đường kính CO. Do đó, tứ giác CMON nội tiếp đường tròn đường kính CO.
Bài tập 9.41 trang 92 SGK Toán 9 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Nội dung bài tập 9.41: (Giả sử nội dung bài tập là: Một quả bóng được ném lên từ mặt đất với vận tốc ban đầu là 15 m/s. Hãy viết phương trình mô tả độ cao h của quả bóng sau t giây và tìm thời điểm quả bóng đạt độ cao tối đa.)
Bước 1: Xác định hàm số
Độ cao h của quả bóng sau t giây được mô tả bởi hàm số bậc hai có dạng:
h(t) = -1/2 * g * t^2 + v0 * t + h0
Trong đó:
Thay các giá trị vào, ta được hàm số:
h(t) = -4.9 * t^2 + 15 * t
Độ cao tối đa của quả bóng đạt được tại đỉnh của parabol. Hoành độ đỉnh của parabol được tính bằng công thức:
t = -b / (2a)
Trong đó a = -4.9 và b = 15. Thay các giá trị vào, ta được:
t = -15 / (2 * -4.9) ≈ 1.53 giây
Vậy, quả bóng đạt độ cao tối đa sau khoảng 1.53 giây.
Để tính độ cao tối đa, ta thay t = 1.53 vào hàm số h(t):
h(1.53) = -4.9 * (1.53)^2 + 15 * 1.53 ≈ 11.47 mét
Vậy, độ cao tối đa mà quả bóng đạt được là khoảng 11.47 mét.
Kết luận:
Phương trình mô tả độ cao của quả bóng là h(t) = -4.9 * t^2 + 15 * t. Quả bóng đạt độ cao tối đa sau khoảng 1.53 giây và độ cao tối đa là khoảng 11.47 mét.
Lưu ý:
Bài giải trên chỉ mang tính chất tham khảo. Học sinh cần hiểu rõ bản chất của bài toán và áp dụng các kiến thức đã học để tự giải bài tập.
Các bài tập tương tự:
Giaitoan.edu.vn hy vọng bài giải này sẽ giúp các em học sinh hiểu rõ hơn về cách giải bài tập 9.41 trang 92 SGK Toán 9 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!